realizată de Arturo Arcos 3 ani în urmă
196
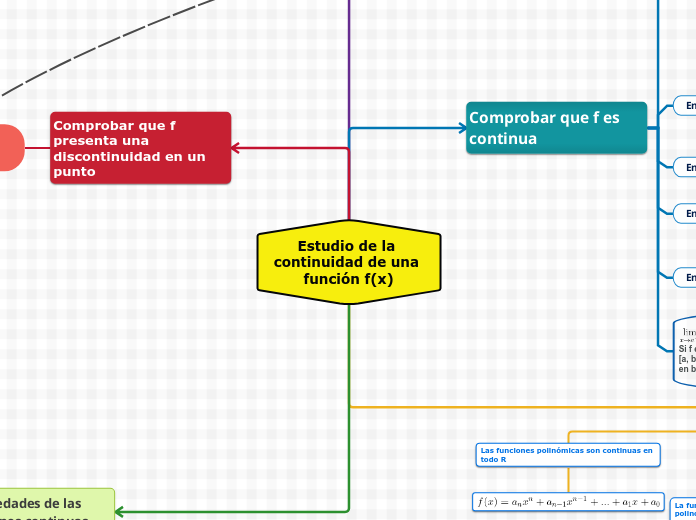
Estudio de la continuidad de una función f(x)
El estudio de la continuidad de una función en un punto específico requiere que se cumplan ciertas condiciones tanto por la derecha como por la izquierda de dicho punto. Para que una función sea continua en un intervalo cerrado, debe ser continua en todos los puntos dentro del intervalo.