realizată de DANIEL SHANG 3 ani în urmă
164
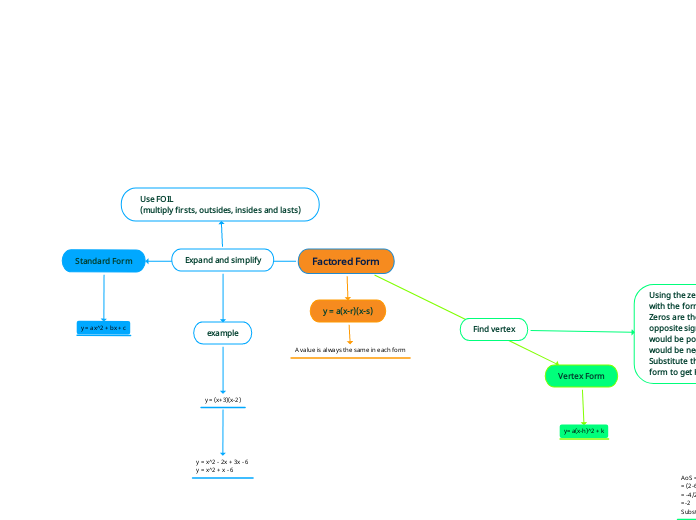
Factored Form
Quadratic equations can be represented in three main forms: factored form, vertex form, and standard form. Each form offers unique insights and methods for solving quadratic equations.
realizată de DANIEL SHANG 3 ani în urmă
164

Mai multe ca aceasta
AoS = (r+s)/2 = (2-6)/2 = -4/2 =-2 Substitute -2 into factored form to get K
Y = 1(-2-2)(2+6) Y = 1(-4)(8) Y = -16 Vertex: (-2,-16)
y = (x+2)^2 - 16