Final Exam - MCR 3U
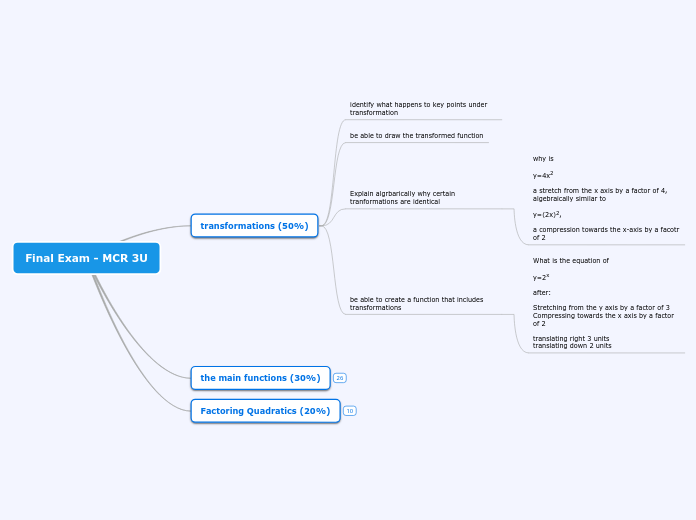
Factoring Quadratics (20%)
meh
solve a quadratic that involves
The quadratic formula
be able to use the discriminant
a tricky trinomial
0=4x2+4x+1
simpe trinomial
0=x2+5x+6
a differnce of squares
0=16x2-25
the main functions (30%)
identify domain and range
of an exponential function
y=2(x+3)+4
of a trig function
y=3sin(2(x+60))+5
of a quadratic
y=(x-2)2+3
be able to create an inverse function
what is the inverse of y=(x-3)^2. Identify the domain and range
what is the inverse of y=2x+5
identify functions or relations
stupid set notation
straight line test
identify the key points for each type of function
y=sqrt(x)
y=sin(x)
be able to state the ratios for the special angles
istem speed test
be able to model with trig functions
be able to create a function with a prescribed amplitude, period, phase shoft and vertical displacement
y=x2
be able to solve using various techniques
y=Bx
be able to work with 1/2 lives
coleum, a medical isotope used to control evil legs, has a 1/2 life of 12 hours.
Create a function to model the amount of coleum at time t, A(t), given the initial amount Ao
coleum a medical isotope has a 1/2 life of 12 hours. What percentage is left after 4 days?
transformations (50%)
be able to create a function that includes transformations
What is the equation of
y=2x
after:
Stretching from the y axis by a factor of 3
Compressing towards the x axis by a factor of 2
translating right 3 units
translating down 2 units
Explain algrbarically why certain tranformations are identical
why is
y=4x2
a stretch from the x axis by a factor of 4, algebraically similar to
y=(2x)2,
a compression towards the x-axis by a facotr of 2
be able to draw the transformed function
identify what happens to key points under transformation