realizată de Jorge Larios 4 ani în urmă
317
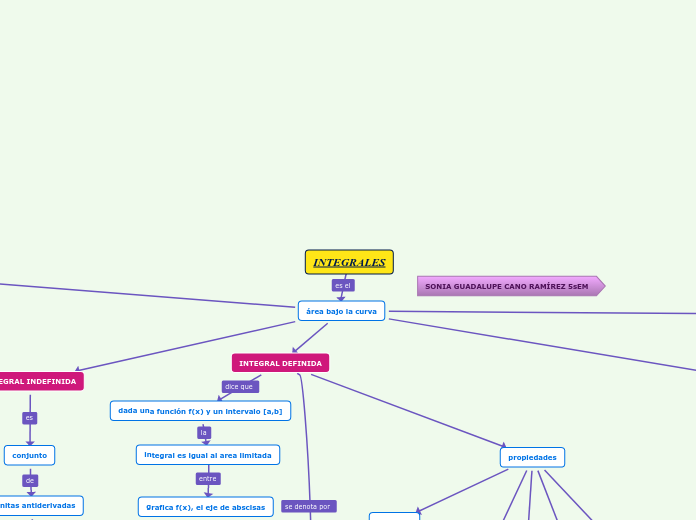
INTEGRALES
El texto aborda conceptos fundamentales del cálculo, centrándose en las integrales y sus aplicaciones. Se describe cómo la integral definida se utiliza para calcular el área bajo una curva, mediante la suma de productos de valores de una función en puntos específicos y los anchos de subintervalos.