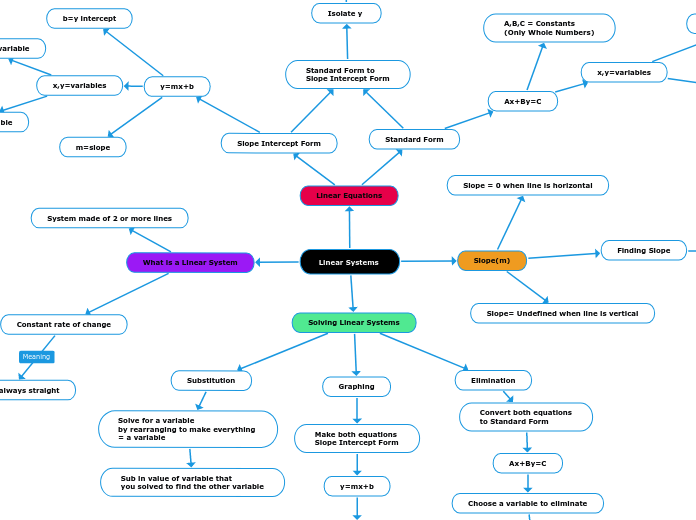
Linear Systems
Slope(m)
Finding Slope
Slope Formula
y2-y1
_____
x2-x1
Slope= Undefined when line is vertical
Slope = 0 when line is horizontal
Linear Equations
Standard Form
Standard Form to
Slope Intercept Form
Isolate y
Move everything to the right
side of the = sign except y
Numbers sign changes when
moved over = sign
2x+y=8
y=-2x+8
Ax+By=C
A,B,C = Constants
(Only Whole Numbers)
Slope Intercept Form
x,y=variables
x = independent variable
y = dependent variable
b=y intercept
m=slope
What is a Linear System
Constant rate of change
Lines are always straight
System made of 2 or more lines
Solving Linear Systems
Elimination
Convert both equations
to Standard Form
Ax+By=C
Choose a variable to eliminate
Multiply both equations by
a number to make the coefficients same or opposite
Add/Subtract the equations to eliminate the
chosen variable
Sub in value of variable that
you solved to find the other variable
Graphing
Make both equations
Slope Intercept Form
y=mx+b
Start each line at y-int(b)
Use the equation of the slope
to draw the lines
If slope is positive, line increases from left-right
If slope is negative, line
decreases from left-right
Substitution
Solve for a variable
by rearranging to make everything
= a variable
Sub in value of variable that
you solved to find the other variable