realizată de David Diaz Zabala 2 ani în urmă
253
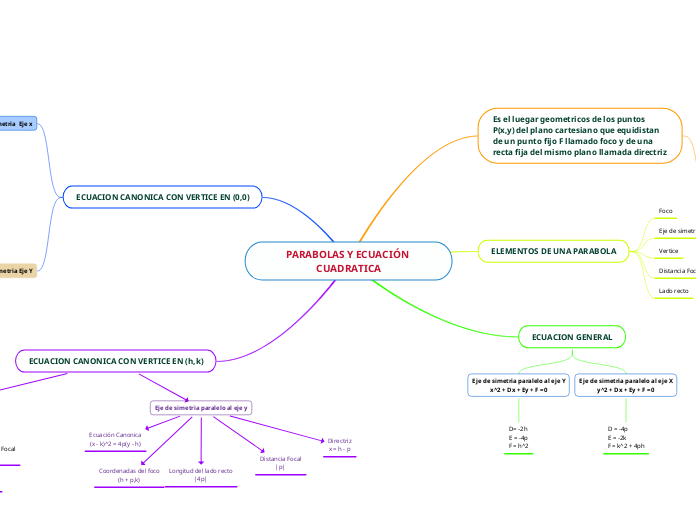
PARABOLAS Y ECUACIÓN CUADRATICA
Una parábola es una curva que se forma a partir de todos los puntos en un plano que están a la misma distancia de un punto fijo llamado foco y una línea fija llamada directriz. La ecuación canónica de una parábola varía dependiendo de la orientación de su eje de simetría y la posición de su vértice.