realizată de Luz Lozano 2 ani în urmă
505
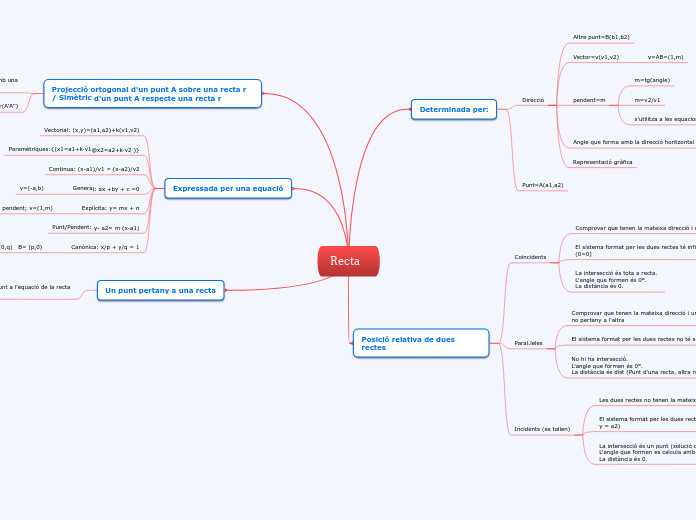
Recta
Una recta es pot determinar per un punt i una direcció, representada gràficament per un vector. La pendent d'una recta és crucial i es calcula com la tangent de l'angle que forma amb l'
realizată de Luz Lozano 2 ani în urmă
505

Mai multe ca aceasta
s'utilitza a les equacions explícita i punt/pendent
m=v2/v1
m=tg(angle)
v=AB=(1,m)