realizată de yanelis barbosa 3 ani în urmă
167
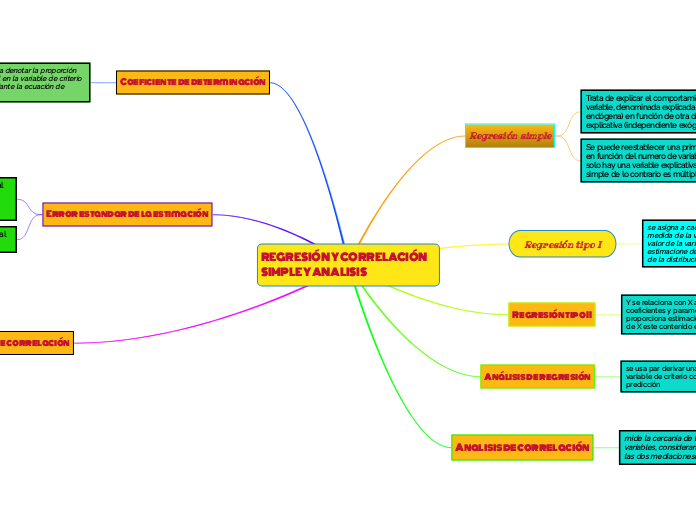
REGRESIÓN Y CORRELACIÓN SIMPLE Y ANALISIS
El estudio de regresión y correlación simple se centra en entender y cuantificar la relación entre variables. El coeficiente de correlación es una medida que indica la fuerza de la relación lineal entre una variable predictiva y una variable de criterio.