realizată de Ashley Bastardo 5 ani în urmă
274
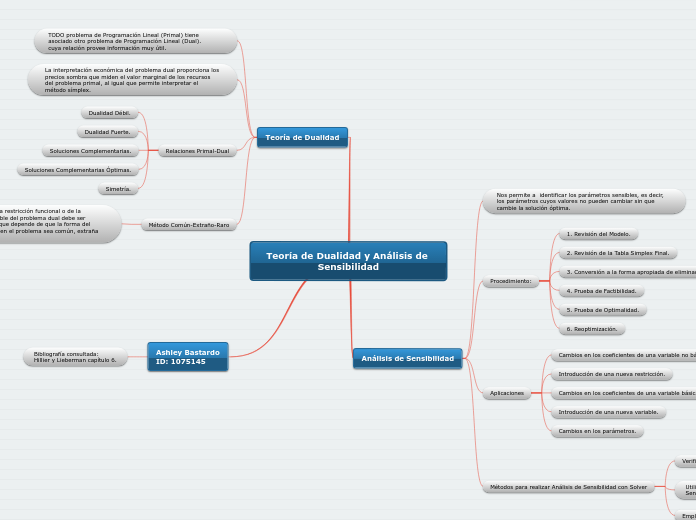
Teoría de Dualidad y Análisis de Sensibilidad
El análisis de sensibilidad es una técnica utilizada para determinar cómo los diferentes valores de los parámetros de un modelo afectan su solución óptima. En particular, se puede utilizar el Solver de Excel para generar tablas de sensibilidad que muestran el efecto de cambios en uno o dos parámetros simultáneamente.