по Camila Giral 6 лет назад
1355
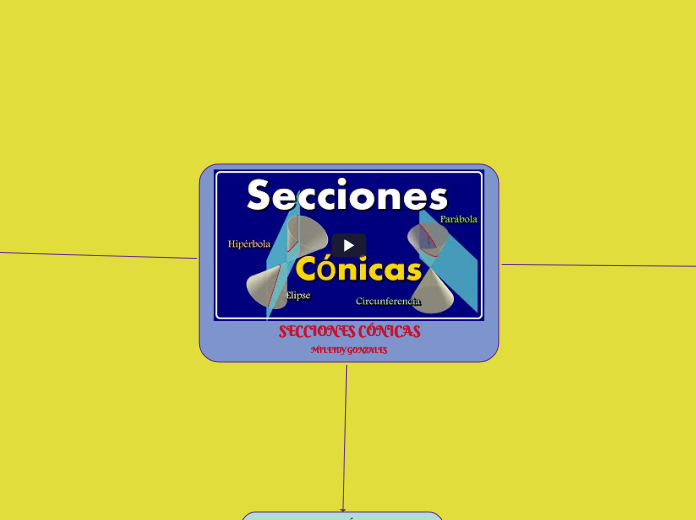
SISTEMA DE COORDENADAS CARTESIANAS
En el sistema de coordenadas cartesianas, las figuras geométricas como la parábola, la elipse y la hipérbola tienen definiciones precisas basadas en la distancia entre puntos específicos y líneas o puntos fijos.