av Vicky Chiu för 15 årar sedan
797
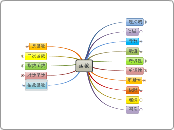
函数
在数学分析中,函数的性质是一个重要的研究领域。函数的定义域决定了函数的取值范围,而函数的奇偶性可以通过对称关系来描述。奇函数在定义域关于原点对称且满足 f(x) = -f(-x),偶函数则满足 f(x) = f(-x)。多项式函数中,奇函数仅包含奇次项,偶函数仅包含偶次项。周期性和单调性也是研究函数行为的重要方面,周期函数在其定义域内重复出现某一模式,而单调函数则在其定义域内保持增减态势不变。
av Vicky Chiu för 15 årar sedan
797

x加绝对值
函数加绝对值
ax,横坐标缩短到原来的1/a倍
2x+3是x向左平移3/2
向下,减
向上,加
向右平移,减
向左平移,加
函数平移相减
点平移相加
满足0/0,或无穷/无穷则可用,f'(x)/g'(x)
(1-1/x)^x=1/e
( 1+1/2x)^x=e^1/2
sin2x/x=2
f(x)=f(-x)
f(x+8)
f(x)
定义域不含0,则f(x)=-f(-x)
定义域包含0,则f(0)=0
f(a)>g(b)恒成立,则f(a)最小值恒大于g(b)最大值
f(x)>g(x)恒成立,则f(x)-g(x)的最小值恒大于0
求法
不存在的值
=0
分类
极小
先减后增
极大
先增后减