Aplicación de la Derivada - Estudio de Funciones

Mer av detta

APORTES DE LA BIOLOGÍA A LA PSICOLOGÍA(jessica blanco)

av Yisel Blanco

OBJETO Y METODO DE LA SOCIOLOGIA

av lisseth rincon

METODOLOGÍA EN SISTEMAS BLANDOS O SUAVES

av Margareth Marin

patrones de medida y las unidades fundamentales suplementarias y derivadas.

av nataly flores

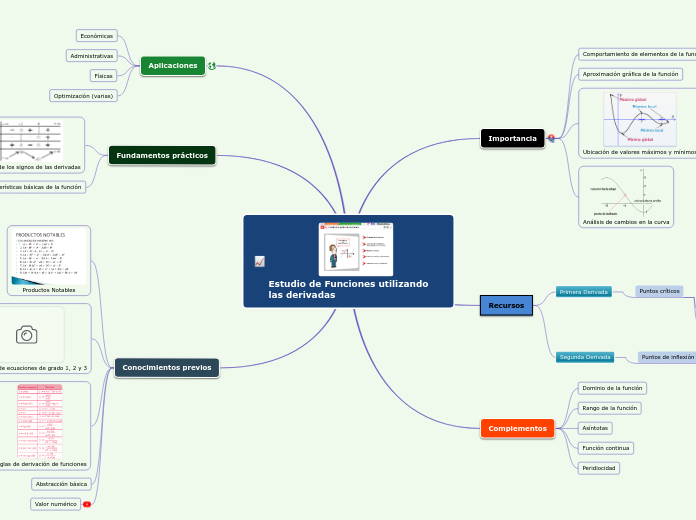
Estudio de Funciones utilizando las derivadas

Conocimientos previos

Valor numérico

Abstracción básica

Reglas de derivación de funciones

Resolución de ecuaciones de grado 1, 2 y 3

Productos Notables

Fundamentos prácticos

Características básicas de la función

Variación de los signos de las derivadas

Aplicaciones

Optimización (varias)

Físicas

Administrativas

Económicas

Complementos

Peridiocidad

Función continua

Asíntotas

Rango de la función

Dominio de la función

Recursos

Segunda Derivada

Puntos de inflexión

Intervalos de convexidad y/o concavidad

Primera Derivada

Puntos críticos

Valores máximos y/o mínimos

Intervalos de crecimiento/decrecimiento de la función

Importancia

Análisis de cambios en la curva

Ubicación de valores máximos y mínimos

Aproximación gráfica de la función

Comportamiento de elementos de la función