av Liza-Mari Carstens för 6 årar sedan
666
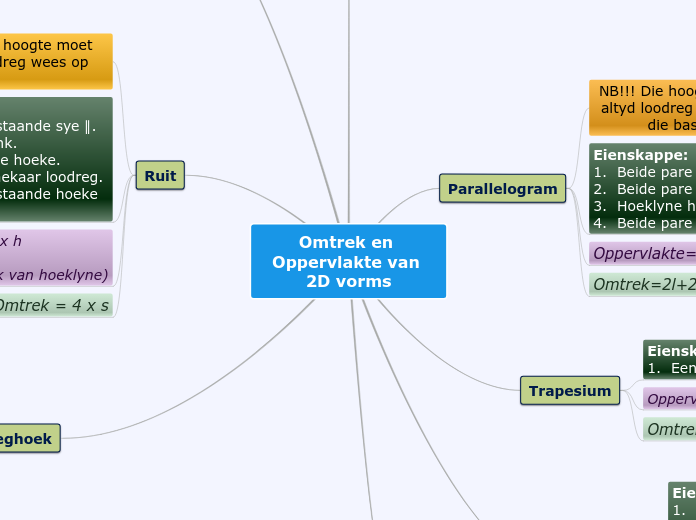
Omtrek en Oppervlakte
In de wiskunde worden verschillende 2D-vormen geanalyseerd op basis van hun eigenschappen, omtrek en oppervlakteformules. Een rechthoek heeft rechte hoeken en gelijke overstaande zijden, terwijl een trapezium één paar parallelle zijden heeft.