av Diana Milena Camargo Rojas för 3 årar sedan
305
Organigrama arbol
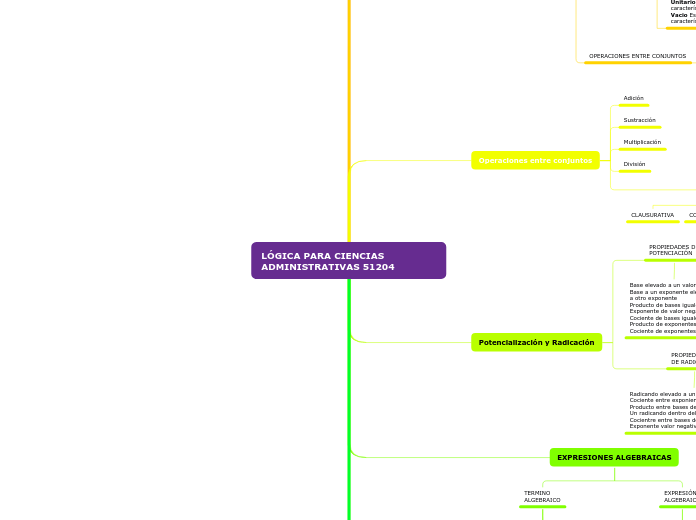
La lógica simbólica y formal es esencial para las ciencias administrativas, permitiendo la construcción de tablas de verdad para evaluar la veracidad de proposiciones. Aristóteles y sus discípulos desarrollaron esta lógica, que se enfoca en la inferencia del conocimiento mediante sistemas deductivos.