av Alejandro Reyes för 7 årar sedan
1375
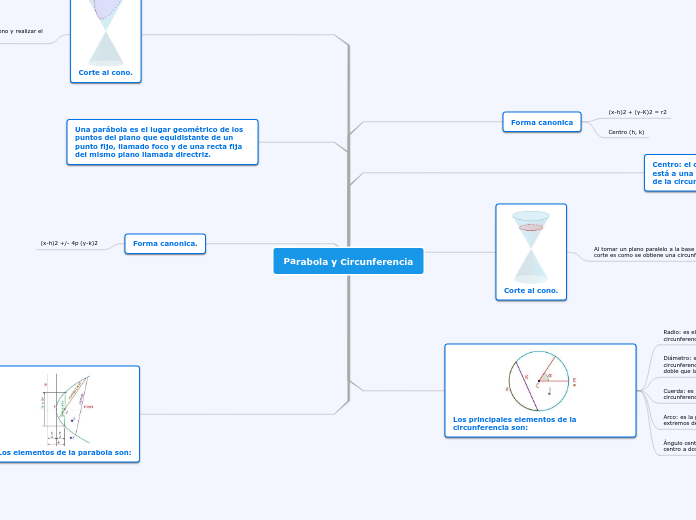
Parabola y Circunferencia
La parábola y la circunferencia son dos figuras geométricas importantes que se obtienen mediante el corte de un cono con un plano. La parábola se define como el conjunto de puntos en un plano que equidistan de un punto fijo, llamado foco, y de una recta fija, denominada directriz.