Pruebas de hipótesis -Modelo de Pearson y Chicuadrado
Prueba de Chi-cuadrado (χ²)RADO
El estadístico chi-cuadrado tomará un valor igual a 0 si existe concordancia perfecta entre las frecuencias observadas y las esperadas; por contra, el estadístico tomará un valor grande si existe una gran discrepancia entre estas frecuencias, y consecuentemente se deberá rechazar la hipótesis nula.
Funcionamiento
Como hemos visto, la prueba chi-cuadrado se utiliza con datos pertenecientes a una escala nominal o superior. A partir de chi-cuadrado, se establece una hipótesis nula que postula una distribución de probabilidad especificada como el modelo matemático de la población que ha generado la muestra.
Una vez tenemos la hipótesis, debemos realizar el contraste, y para ello disponemos de los datos en una tabla de frecuencias. Se indica la frecuencia absoluta observada o empírica para cada valor o intervalo de valores. Entonces, suponiendo que la hipótesis nula es cierta, para cada valor o intervalo de valores se calcula la frecuencia absoluta que cabría esperar o frecuencia esperada.
La prueba chi-cuadrado, también llamada Ji cuadrado (Χ2), se encuentra dentro de las pruebas pertenecientes a la estadística descriptiva, concretamente la estadística descriptiva aplicada al estudio de dos variables. Por su parte, la estadística descriptiva se centra en extraer información sobre la muestra. En cambio, la estadística inferencial extrae información sobre la población.
El nombre de la prueba es propio de la distribución Chi-cuadrado de la probabilidad en la que se basa. Esta prueba fue desarrollada en el año 1900 por Karl Pearson.
Correlación entre variables
Así, como otras pruebas para el mismo fin, la prueba chi-cuadrado se utiliza para ver el sentido de la correlación entre dos variables nominales o de un nivel superior (por ejemplo, la podemos aplicar si queremos conocer si existe relación entre el sexo [ser hombre o mujer] y la presencia de ansiedad [sí o no]).
Para determinar este tipo de relaciones, existe una tabla de frecuencias a consultar (también para otras pruebas como por ejemplo el coeficiente Q de Yule).
Distribución chi-cuadrado
La prueba chi-cuadrado utiliza una aproximación a la distribución chi cuadrado para evaluar la probabilidad de una discrepancia igual o mayor que la que exista entre los datos y las frecuencias esperadas según la hipótesis nula.
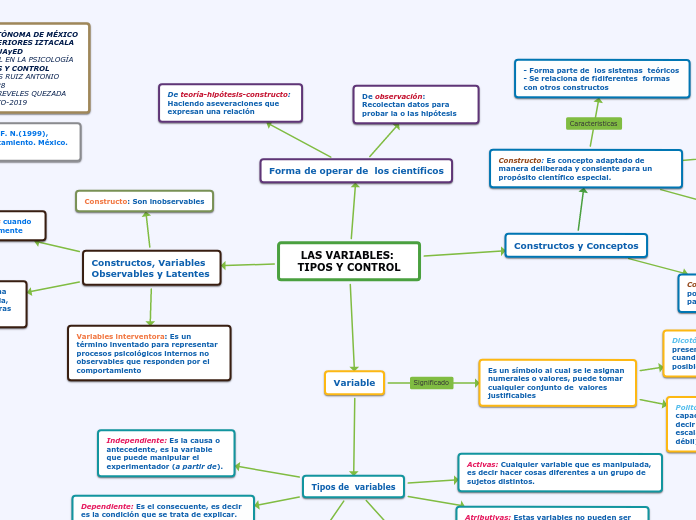
En estadística, existen diversas pruebas para analizar la relación entre variables. Las variables nominales son las que permiten relaciones de igualdad y desigualdad, como por ejemplo el género.
¿Cómo se obtiene la independencia entre variables?
Para evaluar la independencia entre las variables, se calculan los valores que indicarían la independencia absoluta, lo que se denomina “frecuencias esperadas”, comparándolos con las frecuencias de la muestra.
Como es habitual, la hipótesis nula (H0) indica que ambas variables son independientes, mientras que la hipótesis alternativa (H1) indica que las variables tienen algún grado de asociación o relación.
Modelo de Pearson
El coeficiente de correlación de Pearson es una prueba que mide la relación estadística entre dos variables continuas. Si la asociación entre los elementos no es lineal, entonces el coeficiente no se encuentra representado adecuadamente.
El coeficiente de correlación puede tomar un rango de valores de +1 a -1. Un valor de 0 indica que no hay asociación entre las dos variables. Un valor mayor que 0 indica una asociación positiva. Es decir, a medida que aumenta el valor de una variable, también lo hace el valor de la otra. Un valor menor que 0 indica una asociación negativa; es decir, a medida que aumenta el valor de una variable, el valor de la otra disminuye.
Interpretación del coeficiente de correlación de Karl Pearson
El coeficiente de correlación de Pearson tiene el objetivo de indicar cuán asociadas se encuentran dos variables entre sí por lo que:
SubtopicCorrelación mayor a cero: Si la correlación es igual a +1 significa que es positiva perfecta. En este caso significa que la correlación es positiva, es decir, que las variables se correlacionan directamente.
Cuando el valor de una variable es alto, el valor de la otra también lo es, sucede lo mismo cuando son bajos. Si es cercano a +1, el coeficiente será la covariación.
Correlación igual a cero: Cuando la correlación es igual a cero significa que no es posible determinar algún sentido de covariación. Sin embargo, no significa que no exista una relación no lineal entre las variables.
Cuando las variables son independientes significa que estas se encuentra correlacionadas, pero esto nos significa que el resultado sea verdadero.
Correlación menor a cero: Si la correlación es menor a cero, significa que es negativa, es decir, que las variables se relacionan inversamente.
Cuando el valor de alguna variable es alto, el valor de la otra variable es bajo. Mientras más próximo se encuentre a -1, más clara será la covariación extrema. Si el coeficiente es igual a -1, nos referimos a una correlación negativa perfecta.
Cómo se calcula el coeficiente de correlación de Pearson
Donde:
“x” es igual a la variable número uno, “y” pertenece a la variable número dos, “zx” es la desviación estándar de la variable uno, “zy” es la desviación estándar de la variable dos y “N” es es número de datos.
Para llevar a cabo la correlación de Pearson es necesario cumplir lo siguiente:
No debe haber valores atípicos en los datos.
La asociación debe ser lineal.
Las variables deben estar distribuida de forma aproximada.
La escala de medida debe ser una escala de intervalo o relación.
Pruebas de hipótesis
La pruebas de hipótesis evalúan la probabilidad asociada a la hipótesis nula (H0) de que no hay efecto o diferencia. El valor de p obtenido refleja la probabilidad de rechazar la H0 siendo esta verdadera; en ningún caso prueba que la hipótesis alternativa, de que si hay efecto o diferencia, sea verdadera.
La pruebas de hipótesis evalúan la probabilidad asociada a la hipótesis nula (H0) de que no hay efecto o diferencia.
Error tipo I (α) es un falso negativo: rechazar H0 cuando esta es verdadera.
Error tipo II (β) es un falso negativo, aceptar H0 la cuando esta es falsa.
La potencia de un experimento o test describe la probabilidad de detectar una diferencia verdadera de una determinada magnitud.
El valor de p obtenido refleja la probabilidad de rechazar la H0 siendo esta verdadera; en ningún caso prueba que la hipótesis alternativa, de que si hay efecto o diferencia, sea verdadera.
En la inferencia estadística existen dos aproximaciones complementarias: pruebas de hipótesis y estimación.
HIPÓTESIS DE TRABAJO E HIPÓTESIS NULA
EL VALOR DE P
El valor de P es tan ubicuo y tan buscado en la literatura médica que ha llegado a alcanzar poderes mágicos. Feinstein, en su estilo claro e irónico, comenta sobre cómo un acto de juicio científico crítico se convirtió en un templo numérico arbitrario, asombrándose que la comunidad científica haya aceptado tan livianamente una guía que no es ni confiable ni efectiva. La P no es confiable porque depende absolutamente del tamaño de la muestra y esto la hace especialmente peligrosa en los trabajos epidemiológicos. No importa cuán trivial o incluso estúpida sea una hipótesis o cuan pequeña o inconsecuente sea la diferencia que se analiza, los resultados pueden ser estadísticamente significativos si se estudia un número suficiente de casos. La p no es efectiva como guía de la decisión científica, pues el valor de P no tiene que ver con la magnitud de la diferencia que se estudia y, por cierto, la interpretación de significado no debe leerse a partir del valor de P. Es intuitivamente obvio que es un error interpretar un trabajo en forma muy diferente si P resulta 0,048 o bien 0,052.
Entre las preguntas que se pueden contestar con una prueba de hipótesis están las siguientes:
¿Tienen las estudiantes de pregrado una estatura media diferente de 66 pulgadas?
¿Es la desviación estándar de su estatura igual a o menor que 5 pulgadas?
¿Es diferente la estatura de las estudiantes y los estudiantes de pregrado en promedio?
Se puede describir formalmente los pasos a seguir:
Si p es menor que α, rechazar H0 y aceptar la alternativa; en caso contrario, se acepta la hipótesis nula. El conjunto de valores que resultarían en el rechazo de H0 – calculados conociendo la prueba usada, α y el número de observaciones – se conoce con el nombre de región crítica (Figura 1). Este punto puede refrasearse así: se rechaza la H0 si el estadístico cae en la región crítica. En los apéndices de los textos de estadística aparecen tablas con la distribución de estos estadísticos, dando el valor de p y donde el tamaño de la muestra se considera en los grados de libertad.
Calcular el valor de P. Esta es la probabilidad de obtener los resultados observados u otros más extremos si la H0 es verdadera, cifra que es determinada por el área de la distribución que queda más allá del valor calculado.
Elegir el nivel de significación α de la prueba, el límite para rechazar H0. En general, se acepta α = 0,01 ó 0,05, cifras que implican un 1%, o un 5% respectivamente, de posibilidades de equivocarse cuando se rechaza H0, de decir que hay una diferencia cuando en realidad no la hay. Este es el llamado error tipo I.
Elegir la prueba estadística apropiada de acuerdo al diseño experimental, el tipo de datos y el número de grupos que se comparan. La cifra que resulta de usar la prueba (aplicar la o las fórmulas) en los datos recolectados se conoce como el estadístico del test en cuestión: z; estadístico t o de Student, la r de Pearson, F del análisis de varianza, 2. La distribución del estadístico puede ser calculada de antemano cuando la H0 es verdadera y por lo tanto conocer los valores que delimitarán distintas porciones del área bajo la curva de esa distribución; éstas se conocen como distribuciones de muestreo. Vale la pena decir aquí, y lo reiteraremos luego, que las pruebas de hipótesis en ningún caso prueban la veracidad de la hipótesis alternativa o de trabajo, limitándose a decir que no hay suficiente evidencia para rechazar la hipótesis nula basándose en un nivel preestablecido de probabilidades.
Formular la hipótesis y su alternativa. Normalmente la hipótesis de trabajo (por ejemplo, tal tratamiento es mejor que el control o tal procedimiento tiene menos morbilidad) es contrastada con una hipótesis estadística que supone que no existe tal efecto o tal diferencia. La razón para hacer esto es que se puede calcular de antemano la distribución de probabilidades asociadas con tal situación. Esta hipótesis se conoce con el nombre de hipótesis nula que se abrevia como H0 (Nullus: Nula, falto de valor y fuerza para obligar o tener efecto). La expresión matemática es H0: 1= 2. La hipótesis alternativa es que el efecto sí existe, que es distinto de cero, y que en algunos casos se puede especificar el signo de esa diferencia. Normalmente corresponde a la hipótesis de trabajo, se abrevia como H1 y tiene tres alternativas: µ 1≠ µ 2, µ 1< µ 2 o bien µ 1> µ 2