av JEAN CARLOS GRACIANO CONTRERAS för 3 årar sedan
326
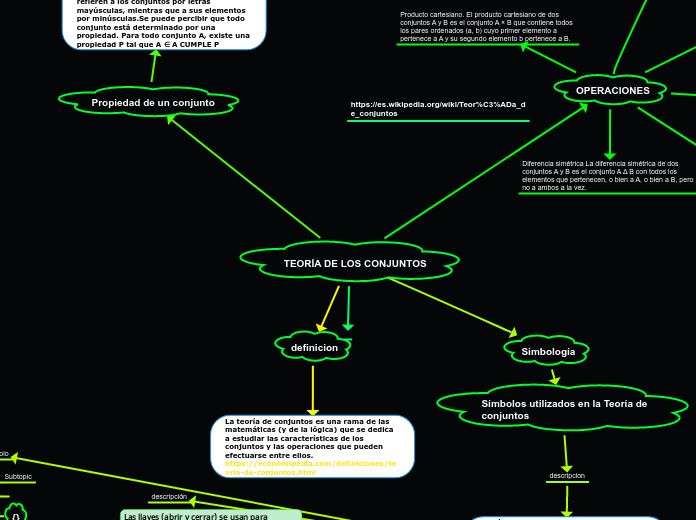
TEORÍA DE LOS CONJUNTOS jean
La teoría de conjuntos es un campo de las matemáticas y la lógica que se dedica a estudiar las características y las operaciones que se pueden realizar sobre los conjuntos. Un conjunto es una colección de objetos, y cada conjunto se define por una propiedad específica que sus elementos cumplen.