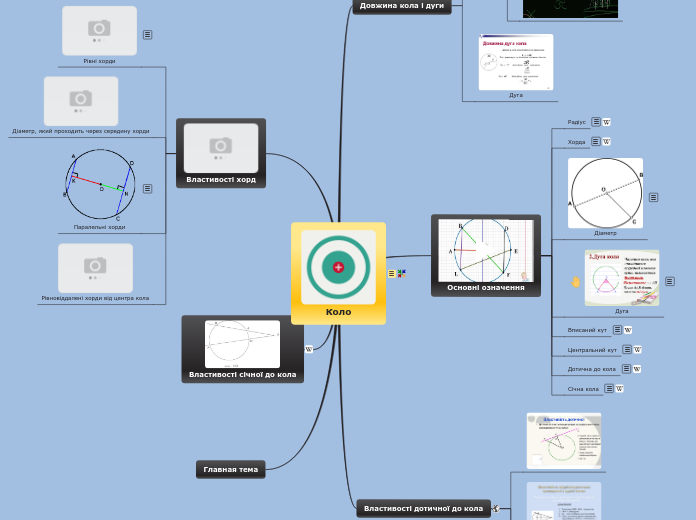
Окружность
Элементы окружности
Диаметр - хорда, проходящая через центр окружности
Хорда - отрезок, соединяющий две произвольные точки окружности
Центр окружности - точка , которая равноудалена от всех точек плоскости и она является не частью, а элементом
Радиус - отрезок, соединяющий точку окружности с ее центром
Взаимное расположение двух окружностей
Две общих точек
S между центрами < R+R2. Расстояние между центрами < радиуса первой окружности + радиус второй окружности
Нет общих точек
S меджу центрами > R - R2. Расснояние между центрами > радиуса первой окружности - радиус второй окружности.
S меджу центрами > R + R2. Расснояние между центрами > радиуса первой окружности + радиус второй окружности.
Касательное
Внутреннее
S между центрами = R+R2. Расстояние между центрами = радиуса первой окружности + радиус второй окружности
Внешнее
S между центрами = R-R2. Расстояние между центрами = радиуса первой окружности - радиус второй окружности
Центральный угол
угол, вершина которого лежит на центре окружности.
Уголок теорем о центральных углах
Теорема №1: Градусная мера центрального угла равна градусной мере други на которую он опирается
Вписанная в треугольньк
Если окружность касается стороны треугольника
Описанная около треугольника
Если окружность проходит через все его вершины
Вписанный угол
угол, вершина которого лежит на окружности, а стороны пересекаются
Уголок теорем о вписанных углах
Теорема №3: Вписанный угол, опирающиеся на диаметр равен 90 градусам
Теорема №1: Вписанный угол равен половине дуги на которую он опирается
Теорема №2: Вписанные углы, опирающиеся на одну и ту же дугу равны
Определение
Геометрическая фигура, состоящая из всех точек плоскости, удаленных от центра окружности на данное расстояние