作者:Мария Сизикова 6 年以前
341
Треугольник
Треугольники классифицируются по различным признакам, включая длины сторон и величины углов. Существуют разносторонние, равнобедренные и равносторонние треугольники, каждый из которых обладает уникальными характеристиками.
開啟
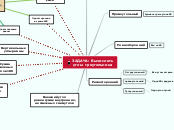
Треугольник Площадь треугольника формула Герона площадь прямоугольного треугольника = половине произведения катетов площадь треугольника = половина произведения стороны и высоты к ней проведенной Признаки подобия по трем сторонам (стороны пропорциональные) по двум сторонам и углу между ними (стороны пропорциональные) по двум углам Признаки равенства по трем сторонам по стороне и прилежащим углам по двум сторонам и углу между ними Общие утверждения Средняя линия треугольника параллельна одной из сторон и равна ее половине Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника медианы треугольника пересекаются в одной точке, которая делит каждую медиану делит в отношении 2:1, считая от вершины биссектрисы и медианы всегда лежат внутри треугольника Внешний угол треугольника равен сумме двух внутренних не смежных с ним Сумма углов в треугольнике равна 180 градусам Виды по сторонам равнобедренный биссектриса,проведенная к основанию является медианой и высотой боковые стороны равны, третья сторона - основание, углы при основании равны равносторонний все стороны равны, все углы по 60 градусов, все биссектрисы являются медианами и высотами разносторонний Виды по углам прямоугольный высота, проведенная из вершины прямого угла, делит треугольник на два треугольника подобных данному. h^2 = ac * bc ; a^2 = ac * c ; b^2 = bc * c медиана проведенная из вершины прямого угла в 2 раза меньше гипотенузы катет, лежащий напротив угла в 30 градусов, в 2 раза меньше гипотенузы теорема Пифагора: квадрат гипотенузы = сумме квадратов катетов один угол прямой, два других острые, острые углы в сумме 90 градусов только одна высота лежит внутри треугольника, а две другие совпадают с катетами подтема
тупоугольный только одна высота лежит внутри треугольника, а две другие вне треугольника остроугольный все высоты лежат внутри треугольника