by Мария Сизикова 6 years ago
341
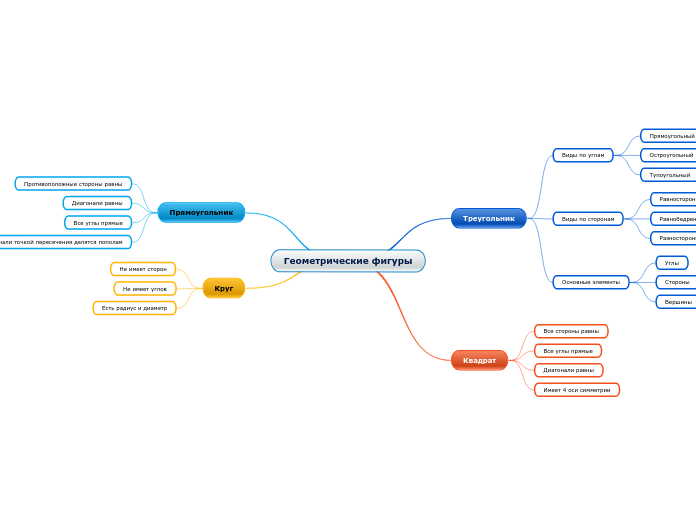
Треугольник
Треугольники классифицируются по различным признакам, включая длины сторон и величины углов. Существуют разносторонние, равнобедренные и равносторонние треугольники, каждый из которых обладает уникальными характеристиками.