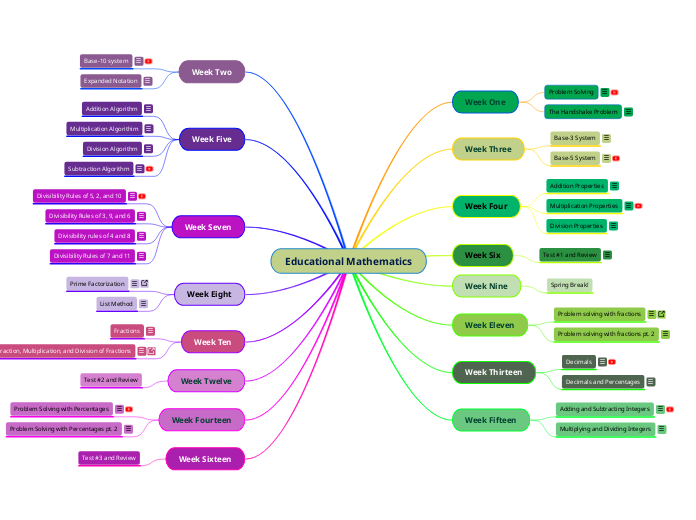
Educational Mathematics
Week Sixteen
Test #3 and Review
Week Fourteen
Problem Solving with Percentages pt. 2
Problem Solving with Percentages
Week Twelve
Test #2 and Review
Week Ten
Addition, Subtraction, Multiplication, and Division of Fractions
In order to subtract and add fractions, prime factorization can be used to find a least common multiple and a common denominator between the two fractions.
For example:
In order to add 1/3 and 1/5, there is a common denominator of 15, we can multiply 1/3 by 5/5 and 1/5 by 3/3 to get 5/15 and 3/15 to get 8/15.
To subtract 5/6 and 1/2, you can find the common denominator of 6, so you can multiply 1/2 by 3/3 and add 5/6 and 3/6 to get 8/6, or 4/3.
To multiply fractions, it is just multiplying fractions normally, but with the knowledge that multiplying fractions will make them smaller. For example, multiplying 1/2 and 1/4 will get 1/8, because you are using part of a part.
To divide fractions, you can use the Keep, Change, Flip method, where you keep the first fraction, change the division sign to a multiplication sign, and then flip the last fraction upside down.
For example if you are dividing 2/3 and 4/5, you would change it to
2/3x5/4 to get 5/6.
Fractions
Meanings of fractions:
Fractions can be a part of a whole or something that has been divided into equal parts, with only a few of those parts being considered.
They can be a quotient: 3 divided by 4= 3/4
They can also represent a ratio, or a part out of a whole
Key points:
Fractional parts are equivalent parts
If the numerator and the denominator are the same, then it equals one whole
The more pieces of something, the smaller the pieces will get
Week Eight
List Method
The list method is a helpful way to write out a list of the factors, and the multiples between two numbers
24: 24, 48, 72
36: 36, 72
Least Common Multiple: 72
Prime Factorization
Week Seven
Divisibility Rules of 7 and 11
To find out if a number is divisible by 7, you take the last digit in a number, multiply it by 2 and subtract it from the first two digits
For example:
826, multiply 6x2 to get 12
Subtract 12 from 82 to get 70
and 70 is divisible by 7
To find out if a number is divisible by 11, use the "chop off" method by taking off the last two digits of the number, and adding them to the remaining number
For example:
29,194, and chopping off 94, then adding it to 385
Then chopping 85 off of 385, and adding it to 3, to get 88, which is divisible by 11
Divisibility rules of 4 and 8
The number is divisible by 4 if the last 2 digits are divisible by 4
Example:
7,128, 28 is divisible by 4, so then 7,128 is divisible by 4
The number is divisible by 8 if the last three digits are divisible by 8
Divisibility Rules of 3, 9, and 6
If the sum of all the digits is divisible by 3 and 9
Example:
If the number is 372, 3+7+2 equals 12, which can be divided by 3, so 372 is divisible by 3
Example:
If the number is 198, 1+9+8 equals 18, which can be divided by 9, so 198 is divisible by 9
If the number is divisible by 2 and 3, then it will be divisible by 6
Example:
If the number is 374, it is divisible by 2 and then added together to be divisible by 3, so it is divisible by 6
Divisibility Rules of 5, 2, and 10
When looking at the last digit of a number, you can tell if it is divisible by certain numbers
By 2: 0,2,4,6,8,10,12,14,16
By 5: 0,5
By 10: 0
Week Five
Subtraction Algorithm
Division Algorithm


Multiplication Algorithim
Addition Algorithm
Week Two
Expanded Notation
Expanded Notation helps teach the placement and the power of each number, something that comes in handy when teaching children.
For example:
456= 400+50+6
= (4x100)+(5x10)+(6x1)
=(4x10^2)+(5x10^1)+(6X10^0)
With the base-ten system, for example, we have ones, tenths, hundredths, thousandths which equals 10^0, 10^1, 10^2, 10^3
With any other system, it is essentially the same
For example:
Base-Five system= ones, fives, twenty-fives, one twenty-fives
5^0, 5^1, 5^2, 5^3
Base-10 system
The Base-10 Numeration System is the number system that we use in schools and in society in general. It represents a one to ten relationship between numbers. Using blocks, this week we showed that units can add up to become other units.
For example:
One unit
Adding ten one units together makes a ten unit
Adding ten of the ten units together makes a 100 unit
Adding 10 100 units together makes a 1000 unit
When looking at a number,
a tenth of a unit is a tenth
a tenth of a tenth is a hundredth
a tenth of a hundredth is a thousandth
There are only specific digits used within each of the numeration systems, and the base ten numbers are 0-9, and then it restarts from 11.
If a base number is not given, then the default is ten.
Week Fifteen
Multiplying and Dividing Integers

When dividing positive and negative integers, it is important to remember inverse operations. The addition is the inverse operation to subtraction and division is the inverse operation to division. When looking at division, use the inverse of multiplication to get the answer.

Adding and Subtracting Integers
Integers: Positive and negative numbers

Week Thirteen
Decimals and Percentages
Decimals
Week Eleven
Problem solving with fractions pt. 2
Problem solving with fractions


Week Nine
Spring Break!
Week Six
Test #1 and Review



Week Four
Division Properties
Division is best known as "repeated subtraction"
For example:
If I have 20 cookies and four plates, how many cookies will go on each plate?
20-4= 16
16-4=12
12-4=8
8-4=4
4-4=0
I subtracted 4 from 20 five times, so I divided 20 by 4 to get 5
Multiplication Properties
Identity Property of Multiplication:
Any number multiplied by 1 is the same number
a*1= a
EX: 7*1=7
Communicative Property of Multiplication:
The order in which the numbers are multiplied does not matter
a*b=b*a
EX: 2*7=7*2
Associative Property of Multiplication:
the grouping property or the grouping of the numbers while multiplying does not matter
(a*b)*c = (b*a)*c=(c*a)*b
Zero Property of Multiplication:
Any number multiplied to zero will always be zero
a*0=0
EX: 3*0=0
17*0=0
"of" will always equal multiplication
For example:
If a farmer has three groups of four apples, how many total apples does he have?
3 groups of apples * four different apples = 12 total apples
Distributive Property of Multiplication:
When I multiply a number by the sum of two other numbers, the outcome will be the same as if you added the partial products
a*(b+c) is equal to (a*b)+(a*c)
For example:
10*(1+2) is equal to (10*1)+(10*2)
Addition Properties
The Identity Property:
Any number added with zero is the same number
a+0=a
EX: 7+0=7
Commutative Property of Addition:
(the order property)
the order in which you add the numbers does not matter
a+b=b+a
Associative Property:
the grouping property
(a+b)+c = (b+c)+a = (a+c)+b
EX: (7+3)+5 =15
(3+5)+7 = 15
*kids don't need to know the property name, just the ideas of each property*
Week Three
Base-5 System
The base-5 system works in the same way as well, with the numbers being:
one's 5^0
five's 5^1
25's 5^2
125's 5^3
The digits available for use are 0,1,2,3,4
EX:
143 base 5
(1*5^2)+(4*5^1)+(3*5^0)
=25+20+3
=48
Base-3 System
The Base 3 system operates on the same principles as the Base-10 System, just with different numbers
In Base-3 you have:
one's 3^0
three's 3^1
nine's 3^3
27's 3^4
The only digits available to use are 0,1,2
EX:
211 base 3
= (2*3^2)+(1*3^1)+(1*3^0)
= (2*9)+ (3*1)+(1*1)
=18+3+1
=22
Week One
The Handshake Problem
There are seven people in a room. If each person shakes another person's hand once, how many handshakes will have been made?
Important: People will not shake hands with the same person twice!
How I solved the problem:
I assigned an alphabet letter to each of the seven people, i.e. A, B, C, D, E, F, G
With each of those people, I started assigning handshakes
A shook hands with B, C, D, E, F, G
B shook hands with C, D, E, F, G
C shook hands with D, E, F, G
D shook hands with E, F, G
E shook hands with F, G
F shook hands with G
The number of handshakes being had decreased by one every time, seeing as we weren't double handshaking. The total number of handshakes that were had is 21 total handshakes.
Problem Solving
Polya's Four-Step Method to Problem Solving is:
- Understand the Problem
- Devise a Plan
- Carry out a plan
- Look back (reflect)
Understand the Problem:
- What are you being asked to do or show?
- How could you restate this problem in your own words?
- What are some ways that you can draw or show what you are being asked?
Devise a plan:
- What are you going to do?
- i.e. draw a picture, act it out, make a graph
Carry out the plan:
- Sometimes it doesn't work the first time, you may have to try again
Look back and Reflect
- Does your answer make sense? (important, especially with younger children)
- Did you answer all of the questions being asked of you?
- What is another way you could have solved this question?