Fundamentos de matemáticas

更多类似内容

Isaac Newton

由Juan Cruz Ortiz

Disciplina de la administracion

由Evelyn Villaseñor

ALGEBRA BOOLEANA

由Miguel Abrego

Tipos de imanes

由Kristina G

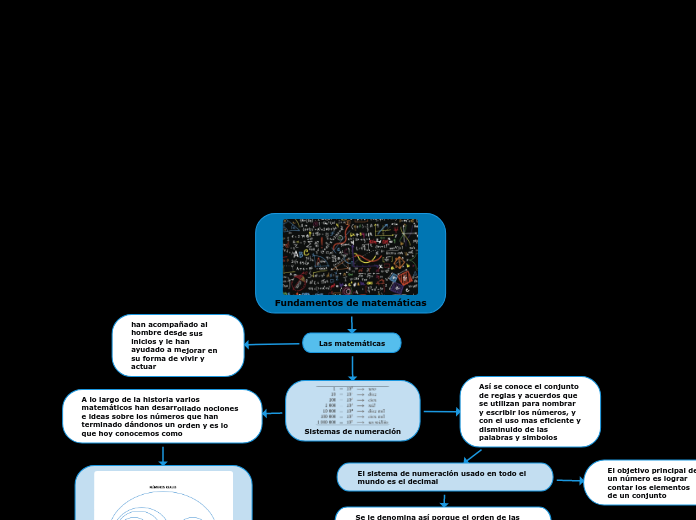
Fundamentos de matemáticas

Las matemáticas

Sistemas de numeración

Así se conoce el conjunto de reglas y acuerdos que se utilizan para nombrar y escribir los números, y con el uso mas eficiente y disminuido de las palabras y simbolos

El sistema de numeración usado en todo el mundo es el decimal

El objetivo principal de un número es lograr contar los elementos de un conjunto

Se le denomina así porque el orden de las unidades aumenta de 10 en 10

El conjunto del sistema decimal está compuesto por 10 elementos

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Cada 10 unidades de un orden es una unidad de orden superios

A lo largo de la historia varios matemáticos han desarrollado nociones e ideas sobre los números que han terminado dándonos un orden y es lo que hoy conocemos como

Números reales

Parte de estos son:

Números racionales

Con estos se puede expresar cosas como; mitad, un tercio, dos cuarto e.t.c.

1/3 5/8 3/16...(Q)

Operaciones posibles:

Resta

División

Suma

Multiplicación

Estos números al igual que los naturales ya eran parte del conocimiento compartido en egipto durante el siglo V a.c (Griegos, Persas y Egipcios)

Para esta época, pitágoras observó que la longitud de la diagonal de un simple cuadrado no podía ser medida con los números racionales y naturales, aún así la diagonal existía y debía tener un número

Fue hasta el tiempo de Euclides (300 a.c) en el que cambió la noción del número pitagórico, entonces si había u número que midiera la diagonal del cuadrado; la raíz cuadrada de 2

Números irracionales

Este fue el nombre dado luego de nacer la raíz cuadrada de 2

También en esta época Euclides demostró que la razón entre la longitud y el diámetro de una circunferencia independientemente de su horario era siempre la misma, constante

incorporó entonces el número

pi

A fines del primer milenio después de Cristo no había números que expresaran las nociones de deuda

Poco a poco fueron surgiendo los

Números negativos

Estos junto a los números naturales formaron

Números enteros

Y a partir del siglo XVI y XVII el desarrollo para las ecuaciones algebraicas de tercer y cuarto grado dio lugar a 3 clases de números

Imaginarios

Nunca formaron parte de los números reales (se integraron a los números complejos)

Los números correspondientes a la raíz cuadrada de u número negativo

Trascendentes

Números que no son raíz de una ecuación algebraica con coeficientes enteros

Algebraicos

Aquellos que son raíz de una ecuación algebraica con coeficientes enteros

Números naturales

Son aquellos que sirven para contar (así se consideran)

0, 1, 2, 3, 4, 5, 6...

Operaciones posibles

Multiplicación A*B=D

Suma A+B=C

han acompañado al hombre desde sus inicios y le han ayudado a mejorar en su forma de vivir y actuar