作者:Amanda Rodrigues 4 年以前
569
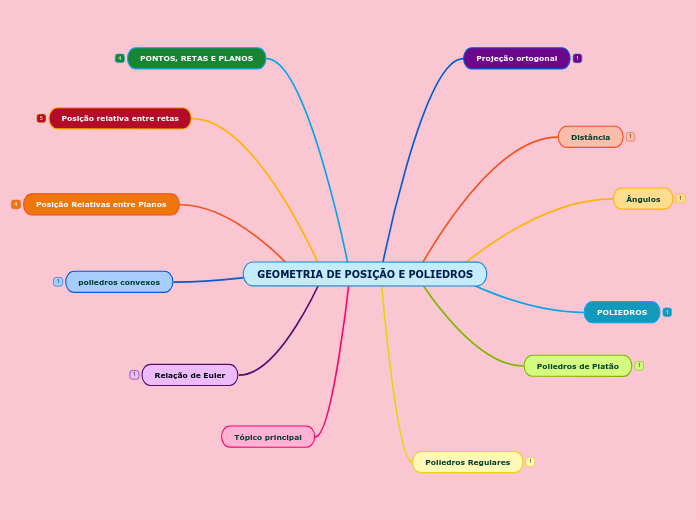
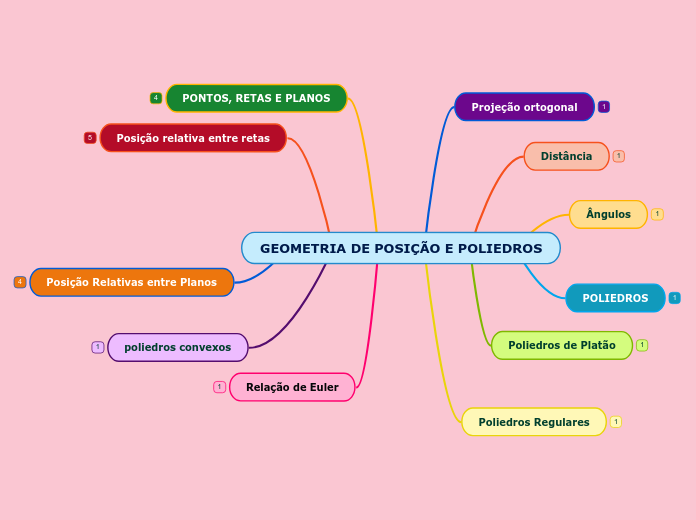
GEOMETRIA DE POSIÇÃO E POLIEDROS
A geometria de posição aborda as relações entre planos e retas, categorizando-os como secantes, coincidentes, perpendiculares, paralelas, concorrentes e reversas, dependendo de como se cruzam ou se alinham.