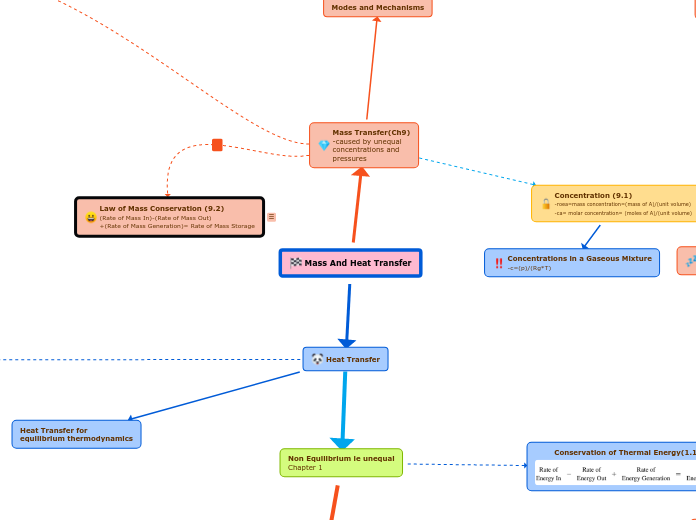
Non Equilibrium ie unequal
Chapter 1
Conservation of Thermal Energy(1.1.3)
Mechanism and Modes
Chapter 2
Mechanisms and modes
Radiative Heat Transfer(2.3)
Where
q=heat flow rate
A=area (m^2)
T=absolute Temp (K)
σ=Stefan-Boltzmann Constant ( 5.676E-8 [W/m^2K^4] or .1714E-8 [Btu/hrft^2R^4 ] )
Diffusion
Conduction(2.1)
Fourier's equation(rate law)
where
k=thermal conductivity of medium (W/mC) or (W/mK)
qx= rate of heat flow in the x direction (W)
T= Temperature at location x (K or C)
x=location in x axis
qx"/A = heat flux
Thermal Diffusivity(2.1.2)
Where
α= thermal diffusivity
ρ= density
cp=specific heat
k=thermal conductivity
flux of energy= α x Gradient in energy
(aka change in internal energy--> different from thermal conductivity because this alone does not determine temp change, also matters how much energy is need for each degree of temp change)
Density and Specific Heat(2.1.3)
-ρ & cp are parts of “thermal mass” of the system.
-ρ x cp=volumetric heat capacity
-two type of density (important when material is porous)
- solid density-mass per unit volume of just the solid portion in porous media
- bulk density- mass of the dried solid to its total volume(solids +pores)
Advection
Convective Heat Transfer(2.2)
Convection over a surface
Where
q1-2 =the heat flow rate from 1-2 (in W or Btu/hr)
A= the area normal to the direction of heat flow (m2 or ft2)
T1 − T2 = the Temp diff b/t surface & fluid
h=the convective heat transfer coefficient, also called the film
coefficient. (W/m^2*C or (Btu/hr*ft^2 *F)
**************Understanding h************************
-This equation is not a law, but rather a defining equation for h.
-h includes the conduction in the fluid in addition to bulk flow
--->presence of conduction(more generally diffusion) will always exist in bulk flow
-h is a function of system geometry, fluid and flow properties, and magnitude of ΔT
Conduction &or Convection
Governing Eqn and Boundary Conditions
Chapter 3
Governing Equation for Heat Transfer (3.1)
if continuity equation is applicable(du/dx=0) then u can be taken out of derivative
**important to realize that the convection term is when the "CV" that our looking at has bulk flow. Different than when a surface has a convection BC
Utility of the equation
- It is useful for any material.
- It is useful for any size or shape. Similar equations can be derived for other coordinate systems.
- It is easier to derive the more general equation and simplify
- It is safer - as you drop terms you are aware of the reasons.
Can we make it more general? (aka its limitations)
- To use with compressible fluids.
- To use when all properties vary with temperature. We need numerical solutions (explained later in the book) to solve such problems.
- To include mass transfer. For example, the equation cannot predict the temperature inside a steak during cooking in an oven since the equation does not include water loss from the steak.
Governing Eq in diff Coordinate Systems(3.5)
doesn't include bulk flow part of general equation
Spherical Coord
Cylindrical Coord
Cartesian Coord
General Boundary Conditions(3.2)
-Boundary Conditions are needed to solve constants of anti-derivatives
-three common types of boundary conditions
2) Surface heat flux is specified
useful in first integral to get first constant (C1)
**surface heat flux is different than internal heat generation
2b) Special case: Symmetry condition
Used in a problem where geometry and the BC are symmetric
---> ex is slab of uniform thickness that is symmetrically cooled
on both sides
x=0 is indicative of the line of symmetry
2a) Special case: Insulated condition
3) Convection at surface
when heat conducted out of the boundary is convected by the fluid
--> the heat flux can only be conducted away as fast as it is
convected away
1) Surface temperature is Specified
Convection Governing Eq & Boundary Conditions
Chapter 6
Info
- Gen Equation in this chapter is applied to fluids instead of solids
- B/c keeping convective term, will work with equations that govern fluid flow
- main goal of chapter is to find h of a fluid
Finding Nu
Forced Convection
Cylinder
the characteristic length is the outside diameter.
********************
over horizontal cylinder
constants B and n are found in table to use in equation
Flow Through Cylinder
characteristic length is the inner diameter of the tube
Flat Plate(6.6.1)
Where
L=distance along the flow
Natural Convection
Flow Over Cylinder assumption
test to use Sphere equation
characteristic length would be the height of the cylinder, L.
D stands for Diameter
***********************************
If D is large enough compared to L can use sphere
*************
for a horizontal circular cylinder
Flow Over Cylinder
Flow Over Sphere
characteristic length is the diameter of the sphere( L becomes D)
Flate plate(6.6.3)
Horizontal surface
The characteristic length in the equations for horizontal plates is calculated as L =A/P, where
A=the surface area
P=the perimeter of the plate.
Hot side facing up or cold side facing down
Hot side facing down or cold side facing up
Vertical surface
characteristic length L is the height of the vertical surface.
Fluid Properties
Film Temperature
Film Temperature is the average Temp of Surface temp and temp of fluid
Film temp is important because it is the temp that you use for a given fluid property like viscosity
Characteristic Length
Characteristic Length (L) depends on the geometry of the surface over which flow takes place
When dimensionless number is denoted with L, it means it is the average number, whereas if it is denoted with x it is the local number
Grashof number
Where
β=Thermal expansion
ΔT= Temp diff( b/t surface and the bulk fluid)
******************************
Grashof number arises because in natural convection velocity of fluid arises from density difference
************************
For ideal gases
β=(1/rho)(P/Rg*T^2) since rho=P/RgT ---> β=1/T
Prandtl Number
Prandtl number relates thermal boundary layer to velocity boundary layer
Nusselt Number
Where
Nu= non-dimensional temperature gradient
Nu compares thermal conduction in the fluid relative to the convection in the fluid.(relates entirely to the fluid and involves fluid thermal conductivity
Convective heat transfer term
(h)
Reynolds Number
Where
μ=viscosity
L= Characteristic Length
uinfinty is the free stream velocity,
x= distance along the flow from the leading edge
*******************
If Reynolds number uses x ---> becomes Rex.
If Reynolds number uses L --> becomes ReL .
If Reynolds number uses D---> becomes ReD.
*******************
Reynolds number is a flow parameter so it depends only on the properties of the fluid( ie velocity density, viscosity) also depends on the distance at which your looking at
Reynolds number related closely to velocity boundary layer
turbulent, laminar, trans for a flat plate?
based on disance x along the plate
Temperature Profiles and Boundary Layers over a Surface(6.2)
Effect of the flat plate on the flow/Temp is essentially restricted to the respectively boundary layers
Thermal BL
Thermal BL eq
Velocity BL
Velocity BL eq
Chapter 5 : Temperature changing with time(not Steady)
Not phase change
Semi Infinite Approx check
5.5 Transient Heat Transfer in Semi-Infinite Region
Governing Eq.
BC Convection at Surface
For specified heat flux condition
Semi-infinite Slab where(h/k is not<<1)
BC Specified Surface Temp
Surface Heat Flux eq, q"
Heat Flux decreases with time
Temp Equation
when (h/k<<1, negligible external resistance)
Biot number
Where
h is the heat transfer coefficient
L is the characteristic length
k is the thermal conductivity
*************
For Bi < 0.1
Eq h(V/A)/k < 0.1
Not negligible internal resistance
Series Solution
Where
α = k/ρcp is the thermal diffusitivity
Fourier Number
Non-dimensional time
*****************
Long time is defined as Fo > 0.2. Substituten n=0
1st Term of Series Solution
Infinite Geometry
-use Heisler Chart to get Temp gradient
-unless special case where we want to find average temp
Boundary Conditions: Surface temp specified
Initial Condition
Ti is the constant initial temperature and Ts is the constant temperature at the two surfaces of the slab at time t > 0.
******************************
Temperature profile will always be symmetric
5.3.3 Avg Temperature Change with Size
For Finite Geometry(5.4)
For a finite cylinder
For a rectangular box
Conditions to use Heisler Chart
Heisler Charts has plots of relations between non-dimensional variables
Where
n=x/L
m=k/hL
Compute with more than one term
Lumped Parameter Analysis
(negligible internal resistance)
When temperature variations are ignored. Temperature would then only vary with time.
********************
Suitable for large surface areas, small volumes, small convective heat transfer coefficients and large thermal conductivities
IC
Freezing and Thawing (Phase Change)
Chapter 7
Evaporation(7.5)
Evaporation from Wet Surfaces(7.5.1)
Where
c stands for concentration of water vapor
hm=mass transfer coefficient
Finding ΔH
Elevated boiling point of slns(7.5.3)
same as in freezing but for boiling point
Freezing
Freezing of Solutions and Biomaterials (7.3)
Where
xA=mole fraction of A(water probably) in the solution
TA0 =freezing point of a pure liquid (K)
ΔHf=the latent heat of fusion
Rg = gas constant ( 8.314 kJ/kmol)
TA=freezing point is the freezing point of the solution in A (K)
Dilute Solutions
Where
xB=mole fraction of B(solute) in the solution
TA0 =freezing point of a pure liquid (K)
ΔHf=the latent heat of fusion
Rg = gas constant ( 8.314 kJ/kmol)
TA=freezing point is the freezing point of the solution in A (K)
also
ΔTf=TA0-TA.
mole fraction xb
mA=mass of water
mB=mass of solute
MA=molecular weight of water
MB= molecular weight of solute
xb=mole fraction for dilute solutions
Where
MA=molecular weight of water
M=molality or moles of solute/unit mass of water(or other solvent)
*****************************
Can use when xB<<1
Temperature Profiles and Freezing Time(7.4)
Heat Loss through a frozen layer
Freezing Time for an Infinite Slab of Pure
Following Assumptions are made
- Initially all material is at freezing temperature Tm but unfrozen.
- All material freezes at one freezing point.
- Thermal conductivity of the frozen part is constant.
working with a symmetric freezing of a slab
convection at surface
Where
Ts=Temp of convective fluid
L=half the thickness
tf=time it takes for all the way to L to freeze
BC that Temp known
Where
x=half the thickness
Tm=initial temp of material
Ts=surface Temp
If working with Biomaterial
Where
λ=heat of fusion
***********
when working wih Biomaterial will give you new ΔH
Temperature not changing with time(Steady)
Chapter 4
Steady-State Heat Transfer from Extended Surfaces:Fins(4.4)
Where
θ=T-Tinfinty .
θb=Tb-Tinfinty .
Tb=Temp at base
m2=(hP)/(kAc)
BC for special case of a long fin
Heat flow eq, q
Fin effectiveness
Steady State Heat Conduction in a Slab with Internal Heat Generation(4.3)
Steady-State Heat Conduction
in a Cylinder(4.2)
Steady-State Heat Conduction in a Slab(4.1)
BC
Heat flow Eq
One Dimensional Conduction through Composite Slab(4.1.1)
Temp Eq
Radiation
Chapter 8
Electromagnetic Radiation
Reflectivity, Absorptivity,Transmissivity
Functions of wavelength
Beer-Lambert Law
Where
Fo=the flux in W/ m^2
δ =the penetration depth, distance at which the flux becomes 1/e
x=distance into material
F=the flux at a location inside the material at a distance x
Radiative Exchange
Where
q= rate of heat flow
F1-2= view angle from body 1->2
two black bodies exchanging
Two gray surfaces create an enclosed volume
Object is completely enclosed in a surface
2 Gray Parallel Infinite Planes
Radiation emitted by a Body
peak emmisive wavelength
Real Body Emission
Total emissitivity ε compares the emissive power E of an actual body to the emissive power of the ideal (black) body
Real Body mono
Monochromatic emissivity = ratio of the monochromatic emissive power of a body to the monochromatic emissive power of a blackbody
*at the same wavelength and temperature
Black Body Emission
Monochromatic emmision
Where
c = is the speed of light
h = Planck's constant (6.625E-34)
κ = Boltzmann's constant (1.380E-23)
T = the absolute temperature in K
Eb_λ,= Energy flux provided by the given wavelength
λ=wavelength
Black Body emmission from range of
wavelengths
The F0−λT values, representing the fraction of total energy emitted by a blackbody at temperature T. Then use equation to find the fraction of energy between the two wavelengths.
Equilibrium between different states of matter(9.3)
Equilibrium between a Gas and a Solid
(With Absorbed Liquid)
-cA,adsorbed=K*c^n_A
ca ,absorbed is the concentration of absorbed solute A
Ca is the concentration of solute A in solution
K* and n are empirical constants
Equilibrium between Solid and Liquid
in Absorption
- 1-RH=b1 exp(-b2w)
-The common example of a solid coming in equilibrium with a gas is the potato chip typically becoming soggy when left out of the package.
where
RH is the relative humidity ( in fraction)
b1 and b2 are constants
and w is the equilibrium moisture content(%)
Concentration (9.1)
-roea=mass concentration=(mass of A)/(unit volume)
-ca= molar concentration= (moles of A)/(unit volume)
roea=ca*Ma
ca in text can means both molar and mass concentration depending on the context unless both are used in one equation
Concentrations in a Gaseous Mixture
-c=(p)/(Rg*T)
Equilibrium Between a Gas and Liquid
-xa=(pa)/H
pa is the partial pressure of species
xa is the concentration of the species
H is the Henry constant ( change base on gas)
Mass And Heat Transfer
Heat Transfer
Heat Transfer for
equilibrium thermodynamics
Table of Contents
Mass Transfer(Ch9)
-caused by unequal
concentrations and
pressures
Modes and Mechanisms
Convective Mass Transfer
studied the same way as Convective Heat Transfer
Convective mass transfer is the movement of mass through a medium as a result of the net motion of a material in the medium
two scenarios
1) Convection-diffusion over a surface and
2) Convection-dispersion in a fluid or porous media.
Convection Dispersion in a fluid orporus media
Convective Diffusion Mass Transfer
Over a Surface
Dispersion Mass Transfer
Dispersion depends on flow, being generally an effect of turbulent flow. Molecular diffusion, due to the thermal-kinetic energy, is always present.
Frick's Law Diffusion
analogous to diffusive heat transfer described in section 2.1
D_AB diffusion coefficient --> mass diffusivity of A in B in m^2/s
analgous to thermal diffusivity
proportionality between diffusive mass flux and concentration gradient
Flux Equation for a convective
Situation
Full General Mass Transfer EQ
Concentration changing with time
semi infinite approx
Semi Infinte
BC and IC
Error Function
not semi infinte appr
Internal Diffusive REsistance
is not negligible
Bi>.1
1D slab
BCs & IC
Internal Diffusive Resistance is Negligible
Bi<.1 (Biot# defined below)
Lumped Parameter
BC
Concentration not changing with time
With Reaction
BCs
The analogy between
the heat and mass transfer situations is quite straightforward. In heat transfer, energy is
diffusing as well as being lost from the surface (decaying). In mass transfer, the species
is diffusing as well as it is decaying as a first order reaction.
no reaction
Multiple Slabs +convection
BCs
One Slab
BCs are
Full General Mass Transfer
Various Coordinate Systems
General Boundary Conditions
Convection at the surface
Surface Mass Flux is
specified
Special Case: Symmetry
Condition
Special Case: Impermeable condition
Surface Concentration is
specificed
Mass average velocty
Capillary Diffusion
cap D os ratio of transport coefficient K and differential capacity
Diffusivity of liquids
(Stokes-Einstein)
Stokes Equation f=6pi(viscosity)r
(mu) is medium viscosity
D is macroscopic diffusion coefficient
f is frictional coefficient
k is boltzman constant
T is absolute Temperature
Diffusivity for gases
where DAB is the diffusivity of A through B,
T is the absolute temperature,
MA and MB are molecular weights,
p is absolute pressure in atm,
σAB is the collision diameter in A
(Omega)D,AB is a dimensionless function of the temperature and the intermolec-ular potential
Diffusivity Speed
Pressure Driven
ch10 Darcy Flow
capillary in a porous solid
H=h+z
n^v is the volume metric flux
H is hydraulic potential or water potential over s distance
K is hydraulic conductivity-represents the ease with which fluid can be transported through a porous matrix,
Redefined Darcy
Redefined K
v_average
φ be the volumetric porosity, (ratio of volume of void space (pore
volume) to the bulk volume of a porous medium.)
Chemical Kinetics(9.4)
generation or depletion of a mass species
nth Rate Law
DEFINITION OF RATE
Rate=(mass of Product produced or reactant consumer)/(Unit volume)(Time)
Law of Mass Conservation (9.2)
(Rate of Mass In)-(Rate of Mass Out)
+(Rate of Mass Generation)= Rate of Mass Storage
this equation is only for one species at a time --> species i