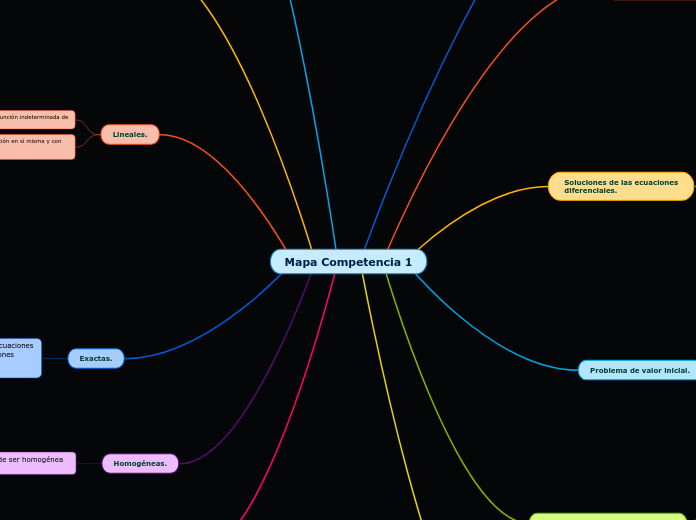
Mapa Competencia 1
Variables separables y reducibles.
El método de separación de variables es una de las varias técnicas utilizadas para
resolver las ecuaciones diferenciales.
Homogéneas.
Una ecuación diferencial puede ser homogénea en dos aspectos.
Oh para el caso lineal de cualquier orden cuando no existen los términos constantes.
cuando los coeficientes de los términos diferenciales en el caso del primer orden son funciones homogéneas de las variables;
Exactas.
Representa una forma general de las ecuaciones
diferenciales a diferencia de las ecuaciones diferenciales homogéneas o las
ecuaciones de Bernoulli.
Lineales.
Relacionada con los valores de la función en sí misma y con sus derivados de
varios órdenes.
Es una ecuación matemática de una función indeterminada de una o varias variables.
De Bernoulli.
La ecuación de Bernoulli es una ecuación diferencial no lineal.
Es llamada una ecuación
diferencial de Bernoulli si el valor de n no es igual a cero o a uno.
Aplicaciones.
Muchos de los problemas de la física como el movimiento de un sistema de masas
unidos a resortes, como también algunos otros problemas prominentes de la
ingeniería, etc.}
Ecuaciones diferenciales ordinarias.
En matemáticas, una ecuación diferencial ordinaria es la ecuación diferencial que relaciona una función desconocida de una variable independiente con sus derivadas.
Teorema de existencia y unicidad.
Subtopic
Una solución única.
Afirma que existe una solución para los pre-requisitos iniciales
provistos de la ecuación diferencial y la solución obtenida
Es una extensión del problema con valor
inicial.
Problema de valor inicial.
Se compone del derivado de una función
indefinida.
Pueden ser de dos tipos principalmente.
Ecuación diferencial parcial.
Ecuación diferencial ordinaria
Soluciones de las ecuaciones
diferenciales.
Es esencial analizar el orden de la ecuación diferencial.
Es llamada también una extensión del
cálculo de integración.
Resolver una ecuación diferencial requiere el conocimiento previo de las técnicas
de integración.
Métodos para resolverlas.
Ecuación diferencial homogénea.
Método de separación de variables
Definiciones (Ecuación
diferencial, orden, grado, linealidad).
Linealidad.
Ecuaciones diferenciales que no se ajustan a
las condiciones antes mencionadas son llamadas ecuaciones diferenciales no
lineales.
Ecuaciones diferenciales no homogéneas
. Ecuaciones diferenciales homogéneas
Ecuación diferencial Cuasi lineal
Grado.
El grado más alto de cualquiera de los
diferenciales en la ecuación diferencial dada es el grado de la ecuación diferencial.
Orden.
El orden más alto de cualquiera de los
diferenciales en la ecuación diferencial dada es el orden de la ecuación diferencial.
Ecuación diferencial.
Contiene también una o
varias variables independientes.
Contiene
la variable dependiente de la ecuación diferencial dada.
Contiene
algunos términos diferenciales.
Teoría preliminar
t como única variable independiente y dos funciones
incógnitas x(t) e y(t).
Relacionan varias funciones incógnitas.
Variables.
Derivadas.
Conjunto de ecuaciones.