作者:BP - 08RC 788108 Tomken Road MS 3 年以前
273
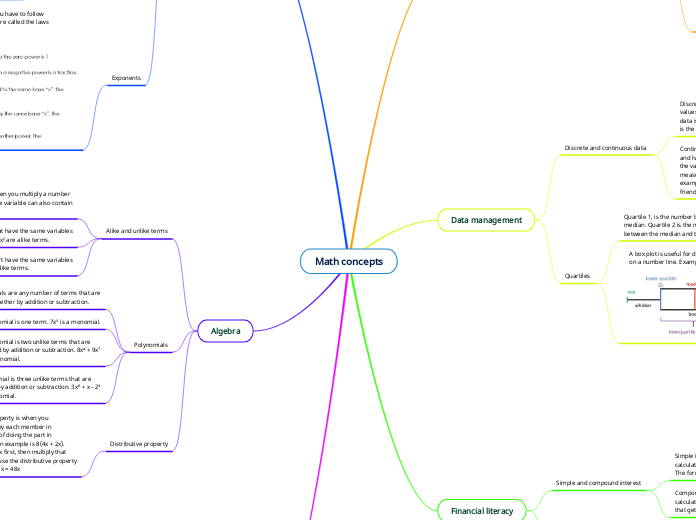
Math concepts
Various mathematical and financial concepts are discussed, starting with quartiles, which divide data into four equal parts. Quartile 1 lies between the minimum and median, Quartile 2 is the median, and Quartile 3 is between the median and maximum.