by BP - 08RC 788108 Tomken Road MS 3 years ago
270
Math concepts
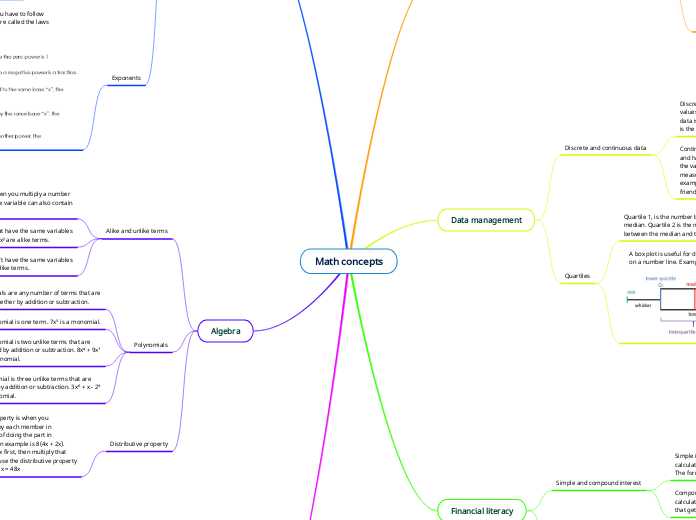
Various mathematical and financial concepts are discussed, starting with quartiles, which divide data into four equal parts. Quartile 1 lies between the minimum and median, Quartile 2 is the median, and Quartile 3 is between the median and maximum.