作者：Amber Johnson 2 年以前
173
更多类似内容
A student takes a test with 45 questions and gets 37 questions right. What percent of the test did she get right?
A factory makes sandals. If they produce 820 sandals a day and 32% of them are blue. How many are blue?
---------------------------------------------------------------------------------------
There are three types of problems:
a) 8 is what percent of 22%
b) 8% of 22 is what number
c) 8% of what number is 22
"is" means =
"of" means to multiply
"what" means the variable of n
change % into decimals and
"what percent" write the decimal as a percent
2.) Marc opened a pizza box. Inside is 3/4 of a pizza. Marc ate 1/2 of what was in the box. How much did he eat?
1.) Janice is prepping a recipe that calls for 3/4 of a cup of oil. If Janice needs to prep 2 and 2/3 servings, how many cups of oil will she need?
3.) If **** represents 2/7 of a whole, draw what the whole looks like.
⭐️Use a rectangle instead of a circle
The video attached is an example video of another problem explaining it mathematically with numbers and using a diagram.
Folding Paper Activity
1/2
-1 second
-1 twoth
a/a * 2/2 is not multiplying by 2 it is multiplying by 1(2/2)
Simplifying
25/100
=5/20 or 1/4
How is the factor 5 different than 25?
When adding numbers you need to find the common denominator.
⭐️Kids will add both numerator and denominator
⭐️multiply numerator by numerator and denominator by denominator
-When you multiple fractions they will get SMALLER
Fractions: An expression :relationship between a part and a whole
3 <- how many pieces were taken
4 <- how many pieces of a whole is divided into
Ways fractions can be used:
Sometimes a fraction is a ration... Vice versa
example: 15 boys and 5 girls = 20 total
15/20 is both a ratio and fraction
5:15 Ratio but not a fraction
(5) part of a whole
Models
⭐️Four Operations before fractions is a NO NO
-When numerate and denominator have the same number it is a whole (1)
-Fractional parts are equivalent parts
-The more pieces I cut the whole into the smaller the pieces get
Addition Algorithms
-American Standard (R to L)
1 1
576
+279
855
-Partial Sums (R to L)
5|7|6
+2|7|9
1|5
1|4
+ 7|.
8 5 5
-Partial Sums (B) ⭐️
-emphasis on place value (R to L)
-Start with explain what the values are and where they go DO NOT start with the 'standard' way
until they know where the values go
5|7|6
+2|7|9
|1|5
1|4|0
+7|0|0
8 5 5
-Left to Right
576 *read as 500+200= 700, 70+70= 140, 6+9=15
+279
700
140
+ 15
855
-Expanded Notation
-place value explicit
100 10
576 500 +70+6
+279 + 200+70+9
855 = 800+ 50+5
Lattice
5 7 6 * Diagnals add (4+1= 5)
+2 7 9
|0/1/1/
/7/4/5|
8 5 5
Four Operation: concept and properties
Addition
-When you add zero to any problem and nothing changes
a, a+0= a
ex: 7+0=7
-For any two numbers (a,b) the order does not matter
a,b a+b = b+a
ex: 3,4 3+4 = 4+3
-The way you group any number does not matter
a,b,c (a+b)+c = (a+)b+c)
ex: 1,2,3 (1+2)+3 = 1+(2+3)
Subtraction
ex: 4 take away 1 =3
-"How many more...?" KEY PHRASE
ex: June has 5 cookies and ate 2. How many more does she have?
-Evon has 4 cookies, mom gave her more. Now she has 7. How many did mom give her?
ex: 4+ ??= 7
-Naturally students will add BUT they should subtract 4 from 7
Multiplication (repeated addition)
:groups of things
3x2= 3 groups of 2 = 6
2 + 2 + 2 (repeated addition)
2 4 6 ( Skip counting)
a, ax1= a
7x1= 7
a,b axb = bxa
7,2 7x2 = 2x7
a,b,c (axb)xc = ax(bxc)
-Any number multiplied by 0 equals zero
a, ax0=0 bx0=0 cx0=0
a,b,c ax(bxc ) = (axb)+(axc)
3+3+3+3
‼️read TOP to BOTTOM‼️
Polya's 4 Steps to Problem-Solving
1.Understand the problem
2.Devise a plan
3.Carry out the plan
4.Look back (reflect)
7 people are strangers and want to shake hands with one another. They must all shake hands ONCE.
Multiplication is REPEATED addition
🚩
Inverse operation
3+4=7 2x3=6
7-3=4 6/3=2
7-4=3 6/2=3
Division
+6/+2=+3 (see diagram in notebook)
+6/+3=+2
Our common number line is the line that is horizontal
⭐️The best way we can help students with integers is if we use a vertical line that way students can make a connection with it like stairs or the floors on a building.
"chip method"
r= (-) Y=(+)
R&Y= zero pair/ They cancel out
Addition
(+5)+(+1)= +6
(-5)+(-1)= -6
(+5)+(-1)= +4 (see notebook for diagrams)
(-5)+(+1)= -4
Subtraction
(+5)-(+1)= -4
(-5)-(-1)= -4 (see notebook for diagrams)
(+5)-(-1)= +6
(-5)-(+1)=-6
multiplication
(+3)x(+2)= +6
(+3)x(-2)= -6
(-3)x(+2)= (+2)x(-3)= -6 (COMMUNITIVE PROPERTY)
(-3)x(-2)=(-2)X(-3). Not possible
sooo... read (-3)x(-2) as the opposite of (-3)x(-2) which is (+3)x(+2) which equals +6
One to 10 base system:
0.123- one hundred twenty three thousands
0.003- three thousandths
$1.03 = 3/100 = 3 pennies = 0.003
3/10 is 3 dimes = 0.3 or 30 pennies
0.8 or 0.95 0.9 or 0.85
8/100 < 95/100 0.90 > 0.85
⭐️when comparing decimals use a grid, money, or drawings
72/100: 0.72 -Seventy two hundredths
31/1000: 0.031 - thirty one thousandths
5/10: 0.5 -five tenths
2/5 = 4/10
-Terminating Decimals : DO NOT repeat
-Repeating number: repeats the same number
-Irrational number: never ends
-ex: 3.14 (pi) not a decimal
-doesn't repeat or terminate
1.) Jim, Ken, Len, and Max have a bag of miniature candy bars from trick-or-treating together. Jim took 1/4 of all the bars, and Ken and Len each took 1/3 of all the bars. Max got the remaining 4 bars. How many bars were in the bag originally? How many bars did Jim, Ken, and Len each get?
So I did 1/4 * 1/3 and got 1/12, this told me that I have to split it into 12ths to find how many bars there were. I then made a diagram split into 4ths and in each 4th I divided it into 3rds. So with this 11/12 bars were shaded. So the last box not shaded was worth 4 bars. So all the boxes are worth 4 bars and so 12 * 4= 48. So there was 48 bars in the bag originally. Jim got 12 bars, Kim got 16 bars, Len got 16 bars and max got 4 bars.
2.) Jim, Ken, Len, and Max have a bag of miniature candy bars from trick-or-treating together. Jim took 1/4 of all the bars. Then Ken took 1/3 of the remaining bars. Next, Len took 1/3 of the remaining bars, and Max took the remaining 8 bars. How many bars were in the bag original? How many bars did Jim, Ken, and Len each get? How is this problem different from problem 1?
So we drew a diagram once again with 4 squares and shaded 1/4 of the bars because Jim took them. Then I did there it was split into 3rs and Ken took a 3rd. Then I divided what was left into sections of 3rds. After since 1 section represents 2 bars then we multiple by the 12 sections and we get 24 bars together. After we count the shaded parts and Jim took 6 bars, Kim took 6 bars, Len took 4 bars, and max took 8. The difference is in one case we are working with parts of the same whole and the other we are working with parts of what's left.
The video attached is an example video of another problem explaining it mathematically with numbers and using a diagram.
24: 1, 2, 3, 4, 6, 8, 12, 24, (composite: Even #)
7: 1, 7 (prime: Odd #)
Why do we use factors?
-To express the product of numbers of prime
-Used for factors like GCF or LCF
36
-multiples of of 36 are 9 times 4
Prime Factor Method:
36= 6x6 24= 12x2
6=3x2 2
6=3x2 12= 6 (3x3) x2
36: 2*2*3*3
24: 2*2*2*3
GCF: 2*2*3 =12
LCF: 12 (2X2X3) *2*3
List method:
24: 1,2,3,6,8,12,14
36: 1,2,3,4,6,9,12,18,36
Multiples:
24, 48, 72,...
36, 72,...
⭐️We need to know this for when doing fractions
Fractions
Greatest Common Factor (GCF)
The Prime Factor Method
ex: 36 6-3 & 2 6- 3& 2
```` 24 2- 2 12- 6-3&2 2
36=2x2x3x3
24= 2x2x2x3
-There are two sets of 2 and one set of 3
-So we multiply 2x2x3 which equals 12= GCF
-To find the lowest common factor we multiply the GCF and the ones that don't pair so 3x2x12 which equal to 72 so that is the LCM
Terms:
Divisibility rule:
Ending 248
-by 2: 0, 2, 4, 6, 8
-by 5: 0, 5
-by 10: 0
sums of digits 248 = 2+4+8=14
-by 3: if sum of digits is divisible by 3
-by 9: if sum of digits is divisible by 9
-by 6: if it is divisible by both 2 & 3
228 ends w/ 8; 2+2+8=12 12/3= 4
Last digits
-by 4: # is divisible by 4 is last 2 digits form a number that is divisible by 4
344: 44/4=11 228: 28/4=7
-by 8: # is divisible by 8 is if the last 3 digits are divisible by 8
-by 7: double the last digit
: subtract the doubled digits with the remaining number
: check to see if it is divisible by 7
-by 11: AKA chop method
: chop last 2 numbers and add it to the remainderg number and repeat until the smallest number is divisibly by 11
Types of symbols
There are multiple things apart of a division
Ex: 11 cookies and 3 plates
11/3 is 3 remainder 2.
The cookies can be divided onto 3 plates and have 3 cookies on each plate. There would be 2 cookies left
Long division
-Standard
-Place Value
Alternate algorithm
2 x 5 =10
|_ _| |_ Product
Factors
Standard
Place value
Lattice
American Standard
European/Mexican
Reverse Indian
Left to right
Integer subtraction
Expanded notation
Ex: 576 to 500+70+6
Base-3
ones : 30
3's : 31
9's : 32
27's. : 33
0,1,2,103,113
a) 10123
=(1x27)+ (0x9)+ (1x3)+ (2x1)
=(1x33)+ (0x32)+ (1x31)+ (2x30)
=27+0+3+2 +32
b) 2213
=(2x9)+ (2x3)+ (1x1)
=(2x33)+ (2x32)+ (1x31)
=18+ 6+ 1 = 25
c) 11013
=(1x27)+ (1x9)+ (0x3)+ (1x1)
=(1x33)+ (1x32)+ (0x31)+ (1x30)
=27+9+0+1 =37
Base? w/ Decimals
21.15 21.115 21.13 21.113
=1/5 =1/25 = 1/3 = 1/9
Base-8
Ones : 80
8's : 81
64's : 82
Compare (< > =)
a)2113 ? 31015
(2x9)+(1x3)+ (1x1) (3x125)+ (1x25)+(0x5)+(1x1)
=18+3+1 =375+25+0+1
=22 > =401
b) 10213 ? 10215
(1x27)+(0x9)+(2x3)+ (1x1) (1x125)+ (0x25)+(2x5)+(1x1)
=27+0+6+1 =125+0+10+1
=34 > =126
130 into a base-5 number
1,5,25,125
130 there are one 125's in 130 so there would be one 5's. in that case it would be 10105
-125
5
19 into a base-3 number
1,3,9,27
19 there are two 9's which equal 18 and 1 left so 2 9's zero 3's and 1 one's = 2013
-.9
10-9= 1
Day 1:
Numeration Systems :Ways to record quantity
-Problem-solving is a process
-US system is a Base-Ten (Decimal systems)
1:10 Relationship
-Position system: where a number sits indicates it's value
Ex: 1,111
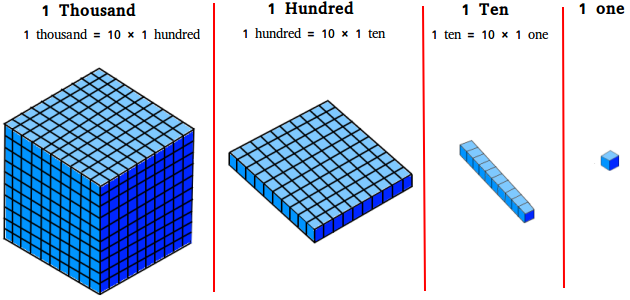
-The number gets bigger when the number moves left x10
-The number gets smaller when the number moves right x10
Decimals
-Separate the function
-ALWAYS sits right of the unit
Expanded Notation
375= 300+70+5
= (3x100)+ (7x10)+ (5x1)
=(3x102)+ (7x101)+ (5x100)
Base-5 Base-10
Ones : 50 Ones : 100
5's : 51 Tens : 101
25's : 52 Hundreds : 102
125's : 53 Thousands : 103
Ex: 2325
= (2x25)+(3x5)+(2x1)
=(2x52)+ (3x51)+(2x50)
= 50+15+2 = 67
Digits used
Base-10: 0,1,2,3,4,5,6,7,8,9,10
Base-5. : 0,1,2,3,4,105,115,125,135,145,205
Example: Use Base-10.
a) 305 b) 2,315 c) 203
= 300+00+5 =2000+300+10+5 = 200+00+3
=(3x100)+(0x10)+(5x1) = (2x1000)+ (3x100)+ (1x10)+ (5x1) = (2x100)+(0x10)+(3x1)
=(3x102)+(3x101)+(3x100) = (2x103)+ (3x102)+ (1x101)+ (5x100) = (2x102)+ (2x101)+ (2x100)
Example: Use Base-5
a) 333 b)43 c)1010
=(3x25)+ (3x5)+ (3x1) =(4x5)+(4x1) =(1x125)+ (0x25)+ (1x5)+ (0x1)
=(3x52)+ (3x51)+ (3x50) =(4x51)+ (3x50) =(1x53)+ (0x52)+ (1x51)+ (0x50)
=75+15+3 =93 =20+ 3 =23 =125+ 0+5+0 = 130
Content: Add, Subtract, Multiply, Divide
Process: Problem-solving
12 Sticks
Move 3 sticks to make 3 boxes
Move 4 sticks to make 3 boxes
Tug-of-war: Acrobats, Grandma, & Ivan
OR
(20 = 20) I=13 I = 2(4) + 1 (5) => 13 = 8 + 5
Discard the Old Books Problem
1st prd. could have 1/6th of the books
2nd prd. could have 1/5th of the books left
3rd prd. could have 1/4th of the books left
4th prd. could have 1/3rd of the books left
5th prd. could have 1/2 of the books left
This left 14 books
6th prd. took to leave no books.
How many books did he have before?
