MTE280🧠🗺
Week 16
Test 3
review
Week 14
A student takes a test with 45 questions and gets 37 questions right. What percent of the test did she get right?
- you would do long division and divide 37 by 45
- you would get .8222 repeating and so you would round up but since the 3rd 2 is not higher than 5 it would stay at a 0.82.
- to turn 0.82 into a decimal you move the decimal 2 times to the right causing you to get 82%.
- So the student got 82% on the test
A factory makes sandals. If they produce 820 sandals a day and 32% of them are blue. How many are blue?
- For this problem you would multiply 820 by 32%
- firs you change the 32% into a fraction by moving the decimal two times to the left so it would be 0.32
- Then you just multiply 820 X .32 which equals 262.40
- So since you can't have 262.40 sandals you would have 262
---------------------------------------------------------------------------------------
There are three types of problems:
a) 8 is what percent of 22%
b) 8% of 22 is what number
c) 8% of what number is 22
"is" means =
"of" means to multiply
"what" means the variable of n
change % into decimals and
"what percent" write the decimal as a percent
Week 12
Test 2
Week 10
Problem Solving w/ Fractions Pt.1
2.) Marc opened a pizza box. Inside is 3/4 of a pizza. Marc ate 1/2 of what was in the box. How much did he eat?
- divide the pizza up into 4ths then divide each 4th into halves which gives us 8th.
- So we know Marc ate 1/2 of the 3/4th pizza
- So Marc ate 1.5 3/4th slice of pizza which is the same as 3/8 slice of pizza
- SO ultimately he ate 3/8
1.) Janice is prepping a recipe that calls for 3/4 of a cup of oil. If Janice needs to prep 2 and 2/3 servings, how many cups of oil will she need?
- 3/4 * 2/3 = 6/12 = 1/2
- She will need 1/2 cups of oil
3.) If **** represents 2/7 of a whole, draw what the whole looks like.
- **** = 2
- **= 1
- So, **************= 7/7
- 14 * equals a whole
⭐️Use a rectangle instead of a circle
The video attached is an example video of another problem explaining it mathematically with numbers and using a diagram.
Week 8
Common Denominator & Numerator
Folding Paper Activity
1/2
-1 second
-1 twoth
- students will refer to 1/2 as 1 second or 1 twoth
a/a * 2/2 is not multiplying by 2 it is multiplying by 1(2/2)
Simplifying
25/100
- divide by a common factor so 5
=5/20 or 1/4
How is the factor 5 different than 25?
- 25 is the greatest common factor
When adding numbers you need to find the common denominator.
- add numerator and leave the denominator
⭐️Kids will add both numerator and denominator
⭐️multiply numerator by numerator and denominator by denominator
-When you multiple fractions they will get SMALLER
Fractions
Fractions: An expression :relationship between a part and a whole
3 <- how many pieces were taken
4 <- how many pieces of a whole is divided into
Ways fractions can be used:
- Part of a whole: 3/4
- Quotient: 3/4
- Ratio 3:4 (most complicated)
Sometimes a fraction is a ration... Vice versa
example: 15 boys and 5 girls = 20 total
15/20 is both a ratio and fraction
5:15 Ratio but not a fraction
(5) part of a whole
Models
- Area (surface)
- length (line model)
- set (groups of things)
⭐️Four Operations before fractions is a NO NO
- student will add across
- will look at denominator as a whole
- 1/2 +2/5 = 3/8 is a NO NO]
- 1/2 < 1/8 will think 1/8 is bigger because 8 is smaller than 2
-When numerate and denominator have the same number it is a whole (1)
- doesn't matter if its a variable a/a=1. xy/xy= 1
-Fractional parts are equivalent parts
-The more pieces I cut the whole into the smaller the pieces get
Week 6
Review
Test 1
Week 4
Addition Algorithms
Addition Algorithms
-American Standard (R to L)
1 1
576
+279
855
-Partial Sums (R to L)
5|7|6
+2|7|9
1|5
1|4
+ 7|.
8 5 5
-Partial Sums (B) ⭐️
-emphasis on place value (R to L)
-Start with explain what the values are and where they go DO NOT start with the 'standard' way
until they know where the values go
5|7|6
+2|7|9
|1|5
1|4|0
+7|0|0
8 5 5
-Left to Right
576 *read as 500+200= 700, 70+70= 140, 6+9=15
+279
700
140
+ 15
855
-Expanded Notation
-place value explicit
100 10
576 500 +70+6
+279 + 200+70+9
855 = 800+ 50+5
Lattice
5 7 6 * Diagnals add (4+1= 5)
+2 7 9
|0/1/1/
/7/4/5|
8 5 5
Four Operations
Four Operation: concept and properties
Addition
-When you add zero to any problem and nothing changes
a, a+0= a
ex: 7+0=7
- Community property: (AKA order property)
-For any two numbers (a,b) the order does not matter
a,b a+b = b+a
ex: 3,4 3+4 = 4+3
- Associative Property (Grouping)
-The way you group any number does not matter
a,b,c (a+b)+c = (a+)b+c)
ex: 1,2,3 (1+2)+3 = 1+(2+3)
Subtraction
ex: 4 take away 1 =3
-"How many more...?" KEY PHRASE
ex: June has 5 cookies and ate 2. How many more does she have?
- Missing Adden (more of a addition problem)
-Evon has 4 cookies, mom gave her more. Now she has 7. How many did mom give her?
ex: 4+ ??= 7
-Naturally students will add BUT they should subtract 4 from 7
Multiplication (repeated addition)
:groups of things
3x2= 3 groups of 2 = 6

2 + 2 + 2 (repeated addition)
2 4 6 ( Skip counting)
a, ax1= a
7x1= 7
a,b axb = bxa
7,2 7x2 = 2x7
a,b,c (axb)xc = ax(bxc)
-Any number multiplied by 0 equals zero
a, ax0=0 bx0=0 cx0=0
a,b,c ax(bxc ) = (axb)+(axc)
 3+3+3+3
3+3+3+3
‼️read TOP to BOTTOM‼️
Week 2
Polya's Steps
Polya's 4 Steps to Problem-Solving
1.Understand the problem
- What do you need to find?
- Restate the problem?
2.Devise a plan
- Guess & Check -> Trial & Error
- Draw Diagrams/ Pictures
- Look for a pattern
3.Carry out the plan
- This is easier than planning
- BE PATIENT! -Most problems aren't solved quickly
- BE PERSISTENT!
4.Look back (reflect)
- Does the answer make sense?
- What did you learn?
7 people are strangers and want to shake hands with one another. They must all shake hands ONCE.
Multiplication is REPEATED addition
- three groups of two
- 2 + 2 + 2 = 6
- 3 x 2 = 6
🚩
- When kids use the first 2 number in a word problem it means they do not understand the task/ problem.
Week 15
Continued...
Inverse operation
3+4=7 2x3=6
7-3=4 6/3=2
7-4=3 6/2=3
Division
+6/+2=+3 (see diagram in notebook)
+6/+3=+2
Integers: + & - numbers
Our common number line is the line that is horizontal
⭐️The best way we can help students with integers is if we use a vertical line that way students can make a connection with it like stairs or the floors on a building.
"chip method"
r= (-) Y=(+)
R&Y= zero pair/ They cancel out
Addition
(+5)+(+1)= +6
(-5)+(-1)= -6
(+5)+(-1)= +4 (see notebook for diagrams)
(-5)+(+1)= -4
Subtraction
(+5)-(+1)= -4
(-5)-(-1)= -4 (see notebook for diagrams)
(+5)-(-1)= +6
(-5)-(+1)=-6
multiplication
(+3)x(+2)= +6
(+3)x(-2)= -6
(-3)x(+2)= (+2)x(-3)= -6 (COMMUNITIVE PROPERTY)
(-3)x(-2)=(-2)X(-3). Not possible
sooo... read (-3)x(-2) as the opposite of (-3)x(-2) which is (+3)x(+2) which equals +6
Week 13
Decimals
One to 10 base system:
- everything RIGHT of the decimal is part of a whole
- everything LEFT of the decimal is a whole getting 10x bigger
0.123- one hundred twenty three thousands
0.003- three thousandths
- the 0 holds the ones & tenths place
$1.03 = 3/100 = 3 pennies = 0.003
- money is a manipulative for decimals
3/10 is 3 dimes = 0.3 or 30 pennies
- the 0 at the end of the decimal doesn't change anything
0.8 or 0.95 0.9 or 0.85
8/100 < 95/100 0.90 > 0.85
⭐️when comparing decimals use a grid, money, or drawings
- they should know place values
72/100: 0.72 -Seventy two hundredths
31/1000: 0.031 - thirty one thousandths
- the 0 is important bc it holds the place value of the tenths
5/10: 0.5 -five tenths
2/5 = 4/10
- easier if fraction has 10, 100, or 1000
- find equivalent fractions w/ 10 or 100
-Terminating Decimals : DO NOT repeat
-Repeating number: repeats the same number
-Irrational number: never ends
-ex: 3.14 (pi) not a decimal
-doesn't repeat or terminate
Week 11
Problem Solving w/ Fractions Pt. 2
1.) Jim, Ken, Len, and Max have a bag of miniature candy bars from trick-or-treating together. Jim took 1/4 of all the bars, and Ken and Len each took 1/3 of all the bars. Max got the remaining 4 bars. How many bars were in the bag originally? How many bars did Jim, Ken, and Len each get?
So I did 1/4 * 1/3 and got 1/12, this told me that I have to split it into 12ths to find how many bars there were. I then made a diagram split into 4ths and in each 4th I divided it into 3rds. So with this 11/12 bars were shaded. So the last box not shaded was worth 4 bars. So all the boxes are worth 4 bars and so 12 * 4= 48. So there was 48 bars in the bag originally. Jim got 12 bars, Kim got 16 bars, Len got 16 bars and max got 4 bars.
2.) Jim, Ken, Len, and Max have a bag of miniature candy bars from trick-or-treating together. Jim took 1/4 of all the bars. Then Ken took 1/3 of the remaining bars. Next, Len took 1/3 of the remaining bars, and Max took the remaining 8 bars. How many bars were in the bag original? How many bars did Jim, Ken, and Len each get? How is this problem different from problem 1?
So we drew a diagram once again with 4 squares and shaded 1/4 of the bars because Jim took them. Then I did there it was split into 3rs and Ken took a 3rd. Then I divided what was left into sections of 3rds. After since 1 section represents 2 bars then we multiple by the 12 sections and we get 24 bars together. After we count the shaded parts and Jim took 6 bars, Kim took 6 bars, Len took 4 bars, and max took 8. The difference is in one case we are working with parts of the same whole and the other we are working with parts of what's left.
The video attached is an example video of another problem explaining it mathematically with numbers and using a diagram.
Week 9
Spring Break
Week 7
Prime Factorization
24: 1, 2, 3, 4, 6, 8, 12, 24, (composite: Even #)
7: 1, 7 (prime: Odd #)
Why do we use factors?
-To express the product of numbers of prime
-Used for factors like GCF or LCF
36
-multiples of of 36 are 9 times 4
- factors of 9: 3 & 3 (3x3=9)
- factors of 4: 2 & 2 (2x2=4)
- =2x2x3x3
- =22x32
Prime Factor Method:
36= 6x6 24= 12x2
6=3x2 2
6=3x2 12= 6 (3x3) x2
36: 2*2*3*3
24: 2*2*2*3
GCF: 2*2*3 =12
LCF: 12 (2X2X3) *2*3
List method:
24: 1,2,3,6,8,12,14
36: 1,2,3,4,6,9,12,18,36
Multiples:
24, 48, 72,...
36, 72,...
⭐️We need to know this for when doing fractions
Fractions
- GCF is used when we simply
- LCM is used to find the common denominator
- 11/12 is the same as 22/24
Greatest Common Factor (GCF)
The Prime Factor Method
- find two multiples
- keep finding multiples until you end with an even number or odd number
ex: 36 6-3 & 2 6- 3& 2
```` 24 2- 2 12- 6-3&2 2
36=2x2x3x3
24= 2x2x2x3
-There are two sets of 2 and one set of 3
-So we multiply 2x2x3 which equals 12= GCF
-To find the lowest common factor we multiply the GCF and the ones that don't pair so 3x2x12 which equal to 72 so that is the LCM
Divisibility
- a is divisible by b if there is a number c that meets this requirement
- c x b = a
- 10 is divisible by 5 ... 2x5=10
Terms:
- 10 is divisible by 5
- 10 is a multiple of 5
- 5 is a divisor of 10
- 5 is a factor of 10
Divisibility rule:
Ending 248
-by 2: 0, 2, 4, 6, 8
-by 5: 0, 5
-by 10: 0
sums of digits 248 = 2+4+8=14
-by 3: if sum of digits is divisible by 3
-by 9: if sum of digits is divisible by 9
-by 6: if it is divisible by both 2 & 3
228 ends w/ 8; 2+2+8=12 12/3= 4
Last digits
-by 4: # is divisible by 4 is last 2 digits form a number that is divisible by 4
344: 44/4=11 228: 28/4=7
-by 8: # is divisible by 8 is if the last 3 digits are divisible by 8
-by 7: double the last digit
: subtract the doubled digits with the remaining number
: check to see if it is divisible by 7
-by 11: AKA chop method
: chop last 2 numbers and add it to the remainderg number and repeat until the smallest number is divisibly by 11
Week 5
Division Algorithm
Types of symbols
- division signs
- division bar aka vanulum
- or the fraction bar ( ?/?)
There are multiple things apart of a division
- quotient is the answer
- dividen is the number inside the vanculum
- remainder is what is left over and can't be divided anymore
Ex: 11 cookies and 3 plates
11/3 is 3 remainder 2.
The cookies can be divided onto 3 plates and have 3 cookies on each plate. There would be 2 cookies left
Long division
-Standard
- just divide the American way
- most common way that is taught
- alot of kids don't know why they do somethings
-Place Value
- more exphasise on the places and where they are coming from
Alternate algorithm
- just do multiples of 10 instead of having to do all the work
- much faster
Multiplication Algorithm
2 x 5 =10
|_ _| |_ Product
Factors
Standard
- multiply like normal and then add
- We add because the top number is 176 five times and the bottom is 176 twenty times
- ex: 176x25
Place value
- 176x25
- 5xx6=30`` 20x6=120
- 5x70=350 20x70=1400
- 5x100=500 10x100= 2000
- =880 =3520
- Add 880+3520 to get 4,400
Lattice
- almost like a punnet square
- add diagonally and read left to right
Subraction Algorithm
American Standard
- right to left
- Use this as the last step to teach subtraction
- student won't fully understand why to cross out the numbers
- they need to understand where they are getting the numbers from
European/Mexican
- right to left
- instead of adding carried numbers to the top add it to the bottom numbers
Reverse Indian
- left to right
- start with subtracting the hundreds then subtract the tens and the ones
- cross out as your going down
- then add the last numbers
Left to right
- left to right
- start with hundreds and write then in the 000 then do tens 00 and ones 0.
- cross out the underside if they need to be reduced
Integer subtraction
- Right to left
- not 4 elementary
- start from the ones then to tens, then hundreds. then reverse subtraction with negative numbers
- ex: 300-10-3 and you will get a positive number
Expanded notation
- place-value explicit
- instead of subtracting in the standard form you would have to change the numbers and change them and give them their value
Ex: 576 to 500+70+6
Week 3
Base-3 & compare
Base-3
ones : 30
3's : 31
9's : 32
27's. : 33
0,1,2,103,113
a) 10123
=(1x27)+ (0x9)+ (1x3)+ (2x1)
=(1x33)+ (0x32)+ (1x31)+ (2x30)
=27+0+3+2 +32
b) 2213
=(2x9)+ (2x3)+ (1x1)
=(2x33)+ (2x32)+ (1x31)
=18+ 6+ 1 = 25
c) 11013
=(1x27)+ (1x9)+ (0x3)+ (1x1)
=(1x33)+ (1x32)+ (0x31)+ (1x30)
=27+9+0+1 =37
Base? w/ Decimals
21.15 21.115 21.13 21.113
=1/5 =1/25 = 1/3 = 1/9
Base-8
Ones : 80
8's : 81
64's : 82
Compare (< > =)
a)2113 ? 31015
(2x9)+(1x3)+ (1x1) (3x125)+ (1x25)+(0x5)+(1x1)
=18+3+1 =375+25+0+1
=22 > =401
b) 10213 ? 10215
(1x27)+(0x9)+(2x3)+ (1x1) (1x125)+ (0x25)+(2x5)+(1x1)
=27+0+6+1 =125+0+10+1
=34 > =126
130 into a base-5 number
1,5,25,125
130 there are one 125's in 130 so there would be one 5's. in that case it would be 10105
-125
5
19 into a base-3 number
1,3,9,27
19 there are two 9's which equal 18 and 1 left so 2 9's zero 3's and 1 one's = 2013
-.9
10-9= 1
Numeration Systems
Day 1:
Numeration Systems :Ways to record quantity
-Problem-solving is a process
-US system is a Base-Ten (Decimal systems)
1:10 Relationship
-Position system: where a number sits indicates it's value
Ex: 1,111
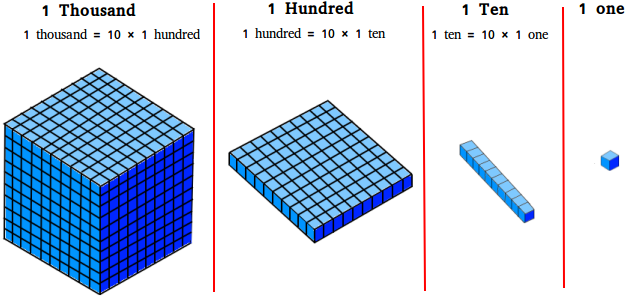
-The number gets bigger when the number moves left x10
-The number gets smaller when the number moves right x10

Decimals
-Separate the function
-ALWAYS sits right of the unit
Expanded Notation
375= 300+70+5
= (3x100)+ (7x10)+ (5x1)
=(3x102)+ (7x101)+ (5x100)
Base-5 Base-10
Ones : 50 Ones : 100
5's : 51 Tens : 101
25's : 52 Hundreds : 102
125's : 53 Thousands : 103
Ex: 2325
= (2x25)+(3x5)+(2x1)
=(2x52)+ (3x51)+(2x50)
= 50+15+2 = 67
Digits used
Base-10: 0,1,2,3,4,5,6,7,8,9,10
Base-5. : 0,1,2,3,4,105,115,125,135,145,205
Example: Use Base-10.
a) 305 b) 2,315 c) 203
= 300+00+5 =2000+300+10+5 = 200+00+3
=(3x100)+(0x10)+(5x1) = (2x1000)+ (3x100)+ (1x10)+ (5x1) = (2x100)+(0x10)+(3x1)
=(3x102)+(3x101)+(3x100) = (2x103)+ (3x102)+ (1x101)+ (5x100) = (2x102)+ (2x101)+ (2x100)
Example: Use Base-5
a) 333 b)43 c)1010
=(3x25)+ (3x5)+ (3x1) =(4x5)+(4x1) =(1x125)+ (0x25)+ (1x5)+ (0x1)
=(3x52)+ (3x51)+ (3x50) =(4x51)+ (3x50) =(1x53)+ (0x52)+ (1x51)+ (0x50)
=75+15+3 =93 =20+ 3 =23 =125+ 0+5+0 = 130
Week 1
Problem-Solving
Content: Add, Subtract, Multiply, Divide
Process: Problem-solving
12 Sticks
Move 3 sticks to make 3 boxes
- Trial & Error => Problem solving => NOT very effective method
Move 4 sticks to make 3 boxes
- Bc you know the first one you tend to do the second one faster.
Tug-of-war: Acrobats, Grandma, & Ivan
- R1: 4A vs. 5G = Draw * Use colored blocks to
- R2: I vs. 2G = Draw demonstrate
- R3: I + 3G = ????
- I + 3G WIN
OR
- R1: 4A = 5G A=5 4(5) = 5(4) => 20 = 20
(20 = 20) I=13 I = 2(4) + 1 (5) => 13 = 8 + 5
- R2: I = 2G + 1A ````` G=4 13 + 3(4) = 4(5) => 13+12= 20
- R3: I + 3G < 4A
Discard the Old Books Problem
- Mr.Smith is getting rid of books by class period
1st prd. could have 1/6th of the books
2nd prd. could have 1/5th of the books left
3rd prd. could have 1/4th of the books left
4th prd. could have 1/3rd of the books left
5th prd. could have 1/2 of the books left
This left 14 books
6th prd. took to leave no books.
How many books did he have before?