作者:Hugo Guarnizo 5 年以前
4235
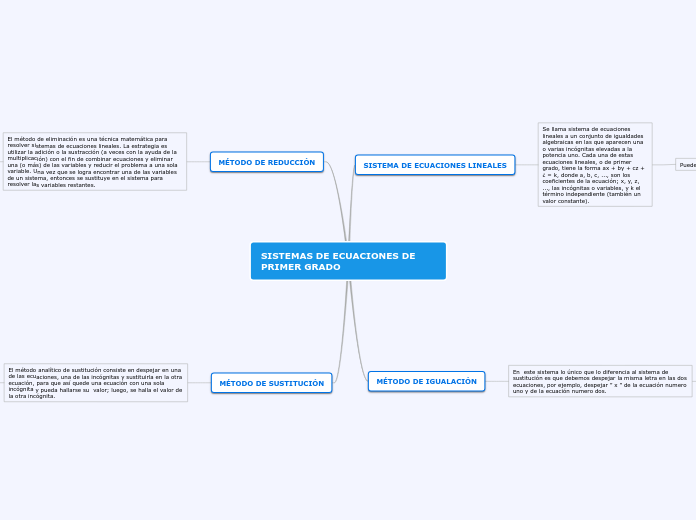
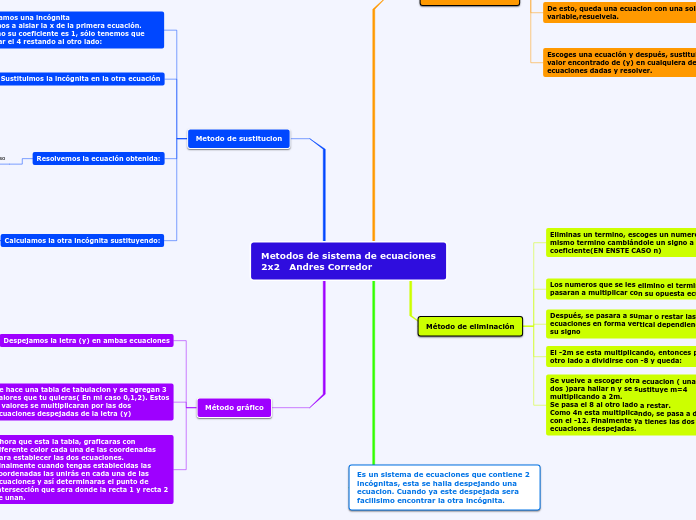
SISTEMAS DE ECUACIONES DE PRIMER GRADO
Resolver sistemas de ecuaciones lineales implica técnicas matemáticas que permiten simplificar y encontrar las variables desconocidas. Entre los métodos más comunes están la eliminación, la sustitución y la igualación.