Geometri 2

Mere som dette

Leserinnlegg uke 11

af Øivind Wiborg

Kreativitet og skaperglede - sikkerhetskopi 090419

af Lene Stigen

Creaza fra Henry_Hk lekse

af Henry Kjærnberg Kjærnberg

geometri

af Ole Marius Ulvøen Forland Forland

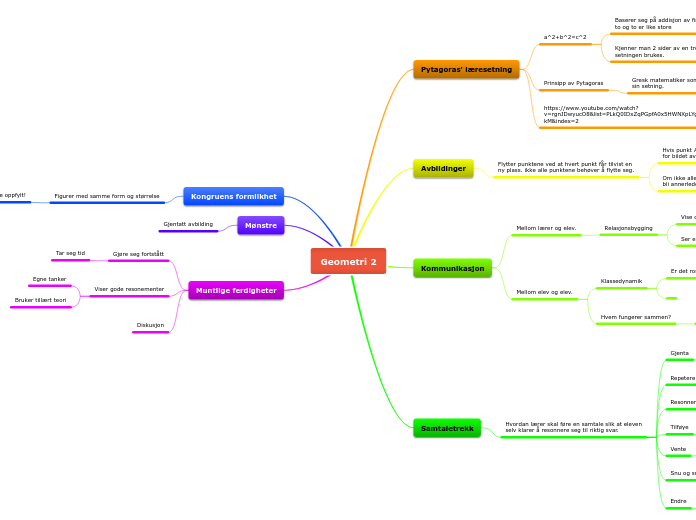
Geometri 2

Muntlige ferdigheter

Diskusjon

Viser gode resonementer

Bruker tillært teori

Egne tanker

Gjøre seg fortstått

Tar seg tid

Mønstre

Gjentatt avbilding

Kongruens formlikhet

Figurer med samme form og størrelse

Denne må være oppfylt!

Samtaletrekk

Hvordan lærer skal føre en samtale slik at eleven selv klarer å resonnere seg til riktig svar.

Endre

Eleven får lov til å endre tenkemåten etter nye innspill.

Snu og snakk

Ber to og to elever om å snakke sammen for å diskutere det som ble sagt.

Vente

Gir eleven tid til å tenke.

Vent i minimum 10 sekunder

Tilføye

Brukes om lærer ønsker mer deltakelse.

Spør ut i rommet om kommentarer

Resonnere

Lærer lar elevene tenke over påstander fra andre elever.

Lærer støtter ikke nødvendigvis påstandene, men støtter opp mot diskusjon.

Repetere

Lærer spør om elev kan gjenta det en annen elev sa.

Kan skape ideer etter å ha hørt hva andre har sagt.

Gjenta

Lærer ber en elev gjenta det en annen elev sa.

Ber andre elever komme med tilbakemelding på det som blir gjentatt

Kommunikasjon

Mellom elev og elev.

Hvem fungerer sammen?

Venner/uvenner?

Klassedynamik

Er det rom for å si feil

Mellom lærer og elev.

Relasjonsbygging

Ser eleven.

Vise omsorg

Avbildinger

Flytter punktene ved at hvert punkt får tilvist en ny plass. ikke alle punktene behøver å flytte seg.

Om ikke alle punktene må flytte på seg kan formen bli annerledes, fra kvadrat rektangel.

Hvis punkt A flyttes til punktet A', kalles A' for bildet av A

Pytagoras' læresetning

https://www.youtube.com/watch?v=rgnJDwyucO8&list=PLkQ0IDxZqPGpfA0x5HWNXpLYgz0z0mrkM&index=2

Prinsipp av Pytagoras

Gresk matematiker som klarte å bevise sin sin setning.

a^2+b^2=c^2

Kjenner man 2 sider av en trekant kan alltid denne setningen brukes.

Baserer seg på addisjon av fire kvadrater hvor to og to er like store