von LISETH VIVIANA RUGELES Vor 4 Jahren
268
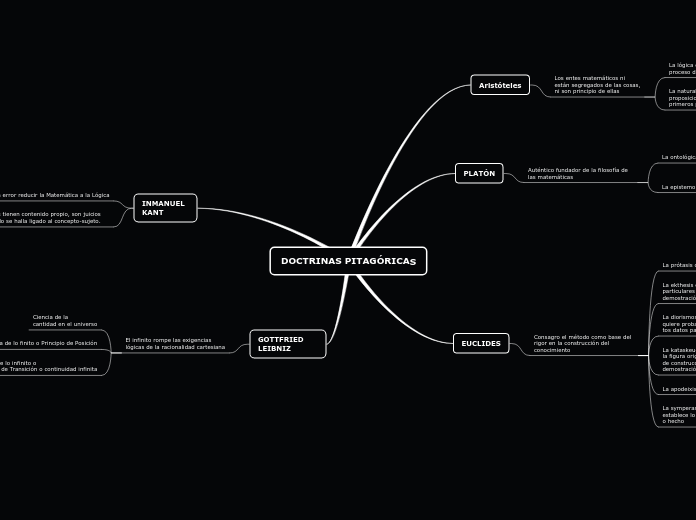
DOCTRINAS PITAGÓRICAS
La filosofía de las matemáticas ha sido moldeada por diversos pensadores a lo largo de la historia. Platón es considerado el auténtico fundador de esta disciplina, enfocándose en aspectos ontológicos y epistemológicos, es decir, la naturaleza de las entidades y la teoría del conocimiento.