von David Páez Vor 2 Jahren
158
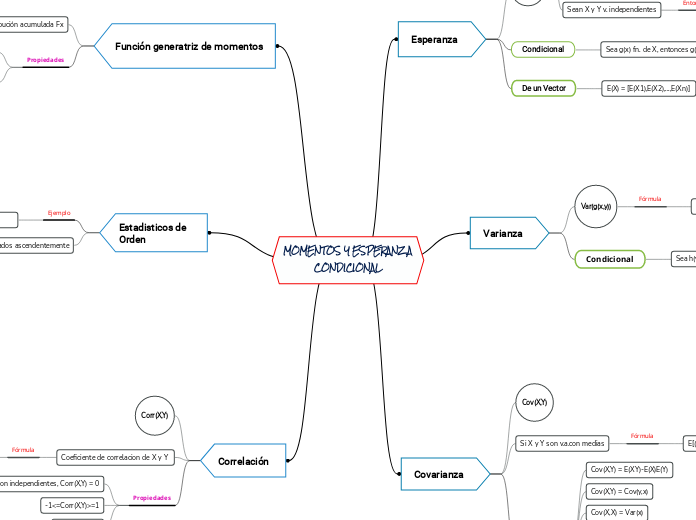
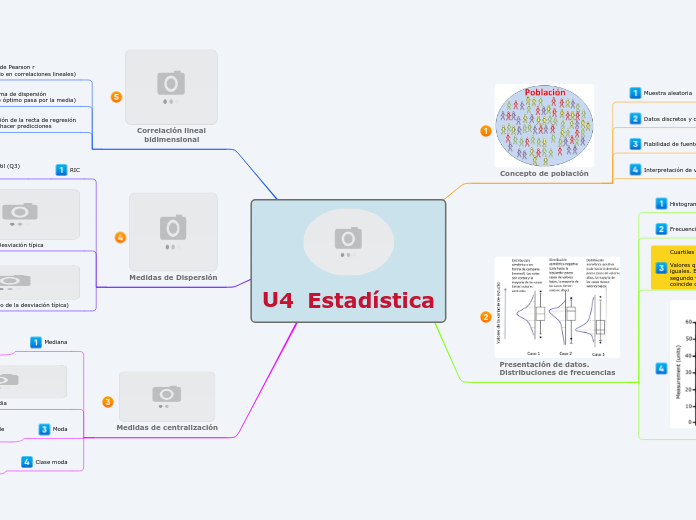
MOMENTOS Y ESPERANZA CONDICIONAL
El texto aborda conceptos fundamentales de la estadística, enfocándose en la correlación, covarianza, varianza y esperanza de variables aleatorias. La correlación mide la relación entre dos variables, con propiedades que incluyen la independencia y el coeficiente de correlación.