von Jorge Sibre Vor 1 Jahr
140
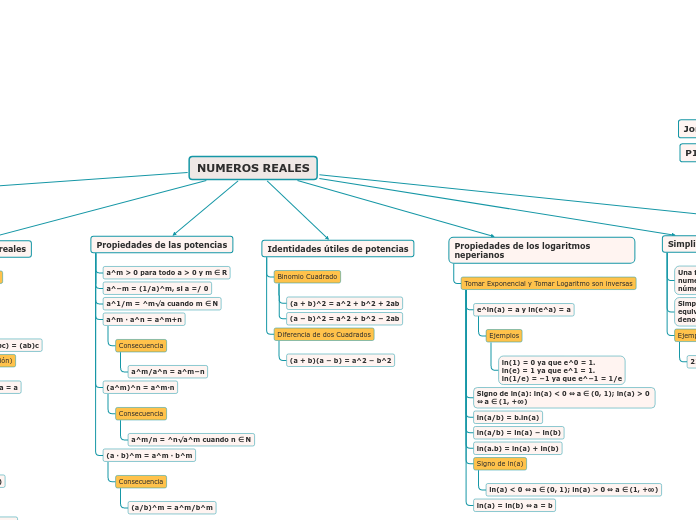
NUMEROS REALES
El texto describe las propiedades fundamentales de los números reales, destacando las características conmutativas y asociativas tanto para la suma como para la multiplicación. También se mencionan los elementos neutros y opuestos en relación con estas operaciones.