P1_PM
Jorge Sibre
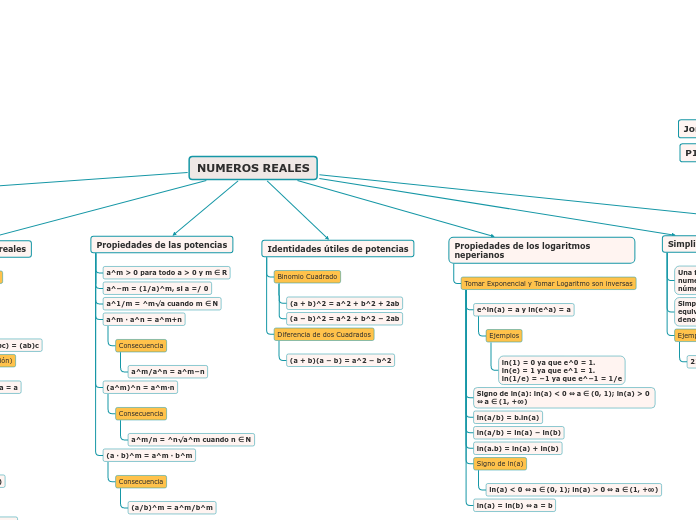
NUMEROS REALES
Simplificación de fracciones
Ejemplo
21/28 = 3 · 7/2^2 · 7 = 3/2^2 = 3/4
Simplificar una fracción es obtener otra equivalente a ella que tenga en el numerador y denominador números más pequeños
Una forma de simplificar una fracción es dividir numerador y denominador por el mismo número
Operaciones con fracciones
Multiplicación de fracciones
El producto de dos fracciones es una nueva
fracción que tiene por denominador el producto de los numeradores y por denominador el producto de los denominadores de las fracciones que se multiplican
a/b . c/d = a . c/b . d
Fracción inversa
La fracción inversa de a/b es b/a
División de fracciones
Para dividir dos fracciones se multiplica la primera
por la inversa de la segunda.
Suma de fracciones
Para sumar dos fracciones con el mismo denominador se suman los numeradores y se deja el denominador común
Para sumar dos fracciones con distinto denominador, primero se reducen a común denominador y después se efectúa la suma
a/b + c/b = a + c/b
Propiedades de los logaritmos neperianos
Tomar Exponencial y Tomar Logaritmo son inversas
ln(a) = ln(b) ⇔ a = b
Signo de ln(a)
ln(a) < 0 ⇔ a ∈ (0, 1); ln(a) > 0 ⇔ a ∈ (1, +∞)
ln(a.b) = ln(a) + ln(b)
ln(a/b) = ln(a) − ln(b)
ln(a/b) = b.ln(a)
Signo de ln(a): ln(a) < 0 ⇔ a ∈ (0, 1); ln(a) > 0 ⇔ a ∈ (1, +∞)
e^ln(a) = a y ln(e^a) = a
Ejemplos
ln(1) = 0 ya que e^0 = 1.
ln(e) = 1 ya que e^1 = 1.
ln(1/e) = −1 ya que e^−1 = 1/e
Identidades útiles de potencias
Diferencia de dos Cuadrados
(a + b)(a − b) = a^2 − b^2
Binomio Cuadrado
(a − b)^2 = a^2 + b^2 − 2ab
(a + b)^2 = a^2 + b^2 + 2ab
Propiedades de las potencias
(a · b)^m = a^m · b^m
(a/b)^m = a^m/b^m
(a^m)^n = a^m·n
a^m/n = ^n√a^m cuando n ∈ N
a^m · a^n = a^m+n
Consecuencia
a^m/a^n = a^m−n
a^1/m = ^m√a cuando m ∈ N
a^−m = (1/a)^m, si a =/ 0
a^m > 0 para todo a > 0 y m ∈ R
Propiedades de los números reales
Distributiva (multiplicación) respecto (Suma)
a(b + c) = a · b + a · c.
Elemento inverso (Multiplicación)
para a =/ 0, a · a−1 = a−1 · a = 1
Consecuencia (División)
a/b significa a · b^−1.
Elemento opuesto (Suma)
a + (−a) = (−a) + a = 0
Consecuencia (Resta)
a − b significa a + (−b)
Elemento neutro (Suma y Multiplicación)
a + 0 = 0 + a = a | a · 1 = 1 · a = a
Asociativa (Suma y Multiplicación)
a + (b + c) = (a + b) + c | a(bc) = (ab)c
Conmutativa (Suma y Multiplicación)
a + b = b + a | ab = ba
Definición
Fracción irreducible
a/b es una fracción irreducible si a y b son primos entre sí
Fracciones equivalentes
a/b y c/d son equivalentes si y s´olo si a.d = b.c
Logaritmo neperiano del número (a)
ln(a) = b ⇔ e^b = a
Potencia de base (a) y exponente (m)
Se denota por am la potencia de base a y exponente m, con a y m ∈ R
Valor absoluto de un n´umero real a que se denota como |a| es
|a| ={ a si x ≥ 0}
{−a si x < 0}
Conjunto de los números reales
R es la unión de los números
racionales e irracionales
Conjunto de los números irracionales
a/b , a, b ∈ Z, b =/ 0
Conjunto de los números racionales:
Q={a/b , a, b ∈ Z, b =/ 0}
Conjunto de los números enteros
Z= {0, ±1, ±2, ±3, . . .}
Conjunto de los números naturales
N= {1, 2, 3, . . .}