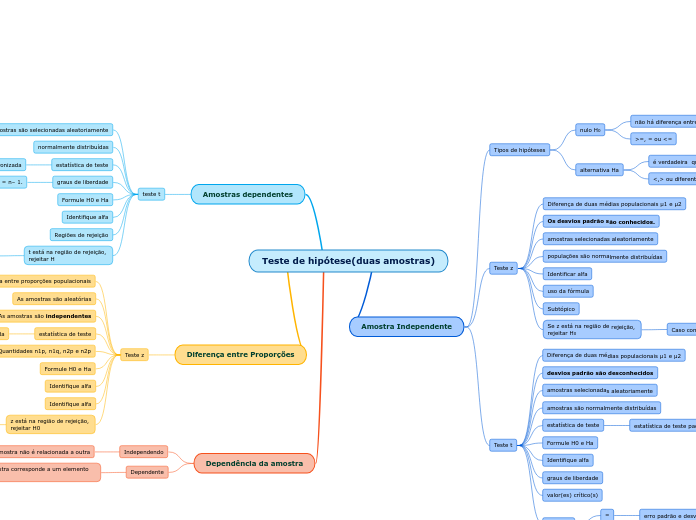
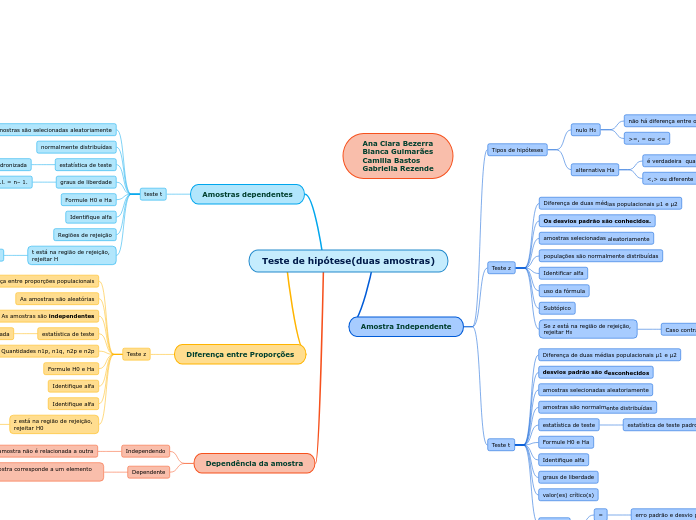
Teste de hipótese(duas amostras)
Dependência da amostra
Dependente
cada elemento de uma amostra corresponde a um elemento de outra amostra
Independendo
uma amostra não é relacionada a outra
Diferença entre Proporções
z está na região de rejeição,
rejeitar H0
Quantidades n1p, n1q, n2p e n2p
Tem que ser ao menos 5
As amostras são independentes
As amostras são aleatórias
a diferença entre proporções populacionais
Amostras dependentes
teste t
t está na região de rejeição,
rejeitar H
Regiões de rejeição
g.l. = n– 1.
normalmente distribuídas
amostras são selecionadas aleatoriamente
Amostra Independente
Teste t
variança
diferente
erro padrão
=
erro padrão e desvio padrão conjunto
valor(es) crítico(s)
graus de liberdade
Identifique alfa
Formule H0 e Ha
estatística de teste
estatística de teste padronizada
amostras são normalmente distribuídas
desvios padrão são desconhecidos
Teste z
Se z está na região de rejeição,
rejeitar H0
Caso contrário, não rejeitar H0
Subtópico
uso da fórmula
Identificar alfa
populações são normalmente distribuídas
amostras selecionadas aleatoriamente
Os desvios padrão são conhecidos.
Diferença de duas médias populacionais μ1 e μ2
Tipos de hipóteses
alternativa Ha
<,> ou diferente
é verdadeira quando H0 é falsa.
nulo H0
>=, = ou <=
não há diferença entre os parâmetros de duas populações