arabera Марина Евгеньевна Гимгина 3 years ago
585
ЗАДАЧА
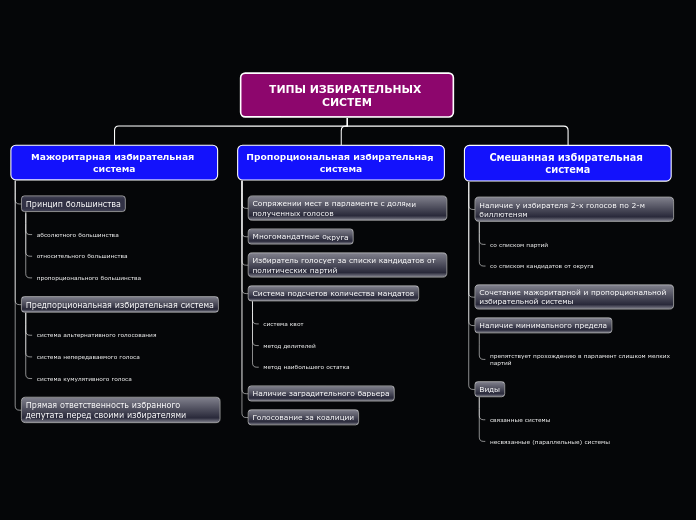
В данном тексте рассматриваются методы распределения мандатов между политическими партиями на выборах. Основное внимание уделяется методу Хэйра и методу д'Ондта. Метод Хэйра основан на квоте, которая вычисляется делением общего числа голосов на количество мандатов.