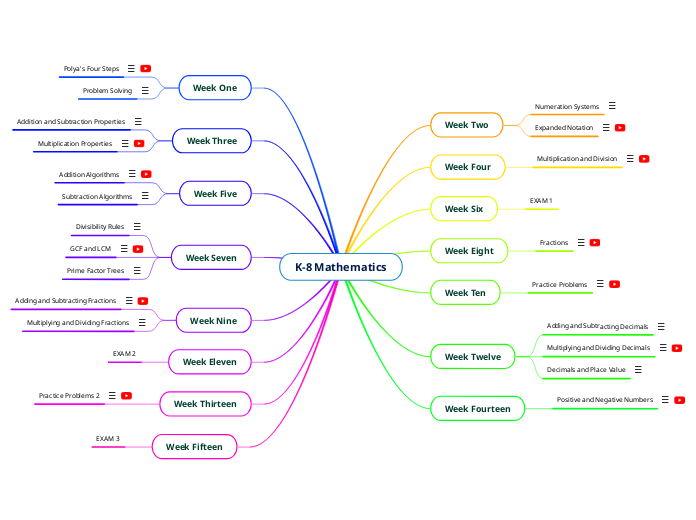
K-8 Mathematics
Week Fifteen
EXAM 3
Week Thirteen
Practice Problems 2
a) 11% of 45 is what number?
0.11 * 45 = 4.95
Multiply the decimal and the whole number together and then add.
b) 9% of what number is 17
0.09 * n = 17
–––– ––––
0.09 0.09
n = 188.8 <–– Repeating decimal / 189
Divide both sides by the decimal.
c) 17% is what % of 25
17/25 = 0.68
|
V
68%
Divide the percentage by the whole number.
Week Eleven
EXAM 2
Week Nine
Multiplying and Dividing Fractions
Multiplication (Part of a Part):
1/2 of 1/2
1/2 x 1/2 = 1/4
1/2 x 1/4 = 1/8
1/3 x 1/8 = 1/24
Division:
2/3 ÷ 4/5 =
(Keep –> Change –> Flip)
2/3 x 5/4 = 10/12 = 5/6
2/3 ÷ 4/5 =
2/3 / 4/5 = 2/3 x 5/4 / 4/5 x 5/4
V V
10/12 20/20 = 1
10/12 / 1 = 10/12 = 5/6
Adding and Subtracting Fractions
Addition:
1/4 + 2/4 = 3/4
3/12 + 2/12 = 5/12
Subtraction:
5/8 - 4/8 = 1/8
8/9 - 2/9 = 6/9 = 2/3
Improper Fractions:
5/6 + 2/3 =
V V
5/6 + 4/6 = 9/6 = 1 3/6 –> 1 1/2 (Mixed Number)
6/10 - 2/5 =
V V
6/10 - 4/10 = 2/10 = 1/5
Week Seven
Prime Factor Trees
Prime Factor Trees
24
/ \
6 4
/ \ / \
3 2 2 2
2 * 2 * 2 * 3 = 24
48
/ \
12 4
/ \ / \
6 2 2 2
/ \
2 3
2 * 2 * 2 * 2 * 3 = 48
GCF and LCM
GCF: Greatest Common Factor
GCF (24, 36):
1. List Method:
24: 1, 2, 3, 4, 6, 8, 12, 24
36: 1, 2, 3, 4, 6, 9, 12, 18, 36
GCF (24, 36) = 12
2. Prime Factorization Method:
*USE TREE*
24: 2 * 2 * 2 * 3
36: 2 * 2 * 3 * 3
GCF (24, 36) = 2 * 2 * 3 = 12
24
/ \
6 4
/ \ / \
3 2 2 2
2 * 2 * 2 * 3 = 24
36
/ \
6 6
/ \ / \
3 2 3 2
2 * 2 * 3 * 3 = 36
LCM: Least Common Multiple
LCM (24, 36):
1.List Method
24: 24, 48, 72, 96
36: 36, 72, 108
LCM (24, 36) = 72
2. Prime Factorization Method
LCM (24, 36) =
GCF * 2 * 3 =
^
Unused Factors from the GCF
12 * 2 * 3 = 72
Divisibility Rules
a is divisible by b if there is a number c that meets the requirement: b * c = a
Ex. 10 is divisible by 5 because 2 * 5 = 10
2 * 5 = 10 5 and 2 are factors of 10
5 * 2 = 10 5 and 2 are divisors of 10
10 ÷ 2 = 5 10 is divisible by 2 and 5
10 ÷ 5 = 2 10 is a multiple of 2 and 5
Divisibility Rules:
Ending:
- By 2: 0, 2, 4, 6, 8
- By 5: 0, 5
- By 10: 0
Sum of Digits:
- By 3: Sum of digits is divisible by 3
- By 9: Sum of digits is divisible by 9
Last Digits:
- By 4: Last two digits are divisible by 4
- By 8: Last three digits are divisible by 8
Extras:
- By 6: If it is divisible by both 2 and 3
- By 7: Double the last digit then subtract from the new number to see if it is divisible by 7.
- By 11: "Chop off", add, check if divisible by 11.
Examples:
*770: 2, 5, 7, 10, 11
*136: 2, 4, 8
Factors:
28: 1, 2, 4, 7, 14, 28
60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
7: 1, 7
91: 1, 7, 13, 91
1 –> Identity Multiplication Element
0 –> Identity Addition Element
Prime Numbers (0-60)
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59
Week Five
Subtraction Algorithms
Subtraction Algorithms
American Standard:
4 13
V V
4 5 3
-2 3 6
––––––
217
European/ Mexican:
1V
4 5 3
4V
-2 3 6
––––––
217
Reverse Indian:
1V
4 5 3
-2 3 6
––––––
2
2
1 7
217
Left - to - right:
13
V
4 5 3
-2 3 6
––––––
2 0 0
2 0
10
7
–––––
217
Expanded Notation:
40 13
453 = 400 + 50 + 3
236 = 200 + 30 + 6
––––––––––––
200 + 10 + 7
217
Integer Subtraction:
4 5 3
-2 3 6
–––––
-3
20
200
––––
217
Addition Algorithms
Addition Algorithms
American Standard:
1
V
384
+235
––––––
619
Partial Sums:
3| 8| 4
+2| 3| 5
––|––|–––
| |9
1 | 1 |
5 | |
––––––––––
619
Partial Sums With Place Value:
3| 8| 4
+2| 3| 5
––|––|–––
| |9
1 | 1 |0
5 | 0 |0
––––––––––
619
Left - to - Right:
384
+235
––––––
500
110
+ 9
––––––
619
Expanded Notation:
100
V
384 = 300 + 80 + 4
+235 = 200 + 30 +5
–––––––––––––––––––
600 + 10 + 9 = 619
Week Three
Multiplication Properties
`Multiplication ––> Repeated addition
3 x 4 = 12 ––> Product
^ ^
Factors
3 x 2 = 3 groups of 2
- Identity property of multiplication
- Any number multiplied by 1, equals one).
- a x 1= a
- 7 x 1 = 7
- -3 x 1 = -3
- 3/5 x 1 = 3/5
- 7 x 0 = 0 (any number multiplied by 0, equals 0).
- Commutative property of multiplication
- The order of numbers being multiplied does not matter.
- a x b = b x a
- 7 x 3 = 3 x 7
- Associative property of multiplication
- When multiplying numbers together in an equation, the grouping does not matter.
- (a x b) x c = a x (b x c)
- (3 x 7) x 2 = 3 x (7 x 2)
- Distributive property of multiplication
- When a number is multiplied by a sum, it is the same as multiplying that number by adding the sum and partial products together.
- a x (b + c) = (a x b) + (a x c)
- 3 x 7 = 3 x (5 + 2) = (3 x 5) + (3 x 2)
Addition and Subtraction Properties
Meaning:
Addition (Put together/ Join)
- Identity Property
- When adding the number 0 to any value, the identity remains the same.
- a + 0 = a
- 4 + 0 = 4
- Commutative Property
- The order of numbers in an equation will equal the same value.
- a + b = b + a
- 3 + 4 = 4 + 3
- Associative Property
- Grouping of numbers does not matter when adding values.
- (a + b) + c = a + (b +c)
Addends
3 + 4 = 7 <–––– Sum
^ ^
Addends
Meanings:
Subtraction:
- Take away (5 - 2 = 3)
- Comparison**
- Missing addend** (3 + __ = 7)
7 - 3 = 4 <–––– Difference
^. ^--- Subtrahend
Minuend
Week One
Problem Solving
I have three 5-cent stamps and two 9-cent stamps. Using one of more of these stamps, how many different amounts of postage can I make?
There are three 5-cent stamps - ©©©
There are also two 9-cent stamps - ©©
©
©©
©©©
©
©©
©©
©©©
©©©
©©©©
©©©©
©©©©©
11 different postage combinations
Explanation: First I started off with laying out the different combinations of the 5-cent and 9-cent stamps, there are three 5-cent (blue) stamps and two 9-cent (red) stamps. Each combination containing both types of stamps are all unique as they have different numbers of both the 5-cent and 9-cent stamps. I first started with different combinations of 5-cent stamps with the 9-cent stamps by adding one, two, or three 5-cent stamps to each combination of 9-cent stamps. For example, when I had one 5-cent stamp I needed to add one 9-cent stamp and then another 9-cent stamp to a different 5-cent stamp so it went up +1 each time until I ran out of 9-cent stamps. I did this with other combinations of 5-cent stamps such as having two or three 5-cent stamps with one or two 9-cent stamps. Adding up all the different combinations of stamps it is a total of 11 different postage combinations.
Polya's Four Steps
- Understand the question/ problem:
- What are you asked to find/ show?
- Can you restate the problem?
- Can you draw a picture or diagram to help you solve the problem?
- Plan how to solve the problem:
- Draw a picture/ diagram
- Look for a pattern
- Work backwards
- Make the problem simpler
- Implement the plan to solve the problem:
- Try different strategies
- Do not get discouraged
- Carrying out the plan is usually easier than devising the plan
- Look back (reflect):
- Is it a reasonable answer?
- Did all questions get answered?
- Is there an easier way?
- What did you learn?
Week Fourteen
Positive and Negative Numbers
-17 + (10) = -7
-10 - (8) = -18
3 * (-4) = -7
16 / -4 = -4
Week Twelve
Decimals and Place Value
Decimals:
a) 0.128 < 0.234 < 0.45 <0.9
b) 0.23 < 0.3 < 0.378 < 0.98
c) 0.003 < 0.03 < 0.033 < 0.303 < 0.33 < 3.003
Place Value:
Hundred Hundred
Thousands Thousands Tens Tenths Thousandths Thousandths
V V V V v V
100,000 10,000 1,000 100 10 1 . 1/10 1/100 1/1,000 1/10,000 1/100,000
^ ^ ^ ^ ^
Ten Hundreds Ones Hundredths Ten
Thousands Thousandths
**If decimals are repeating, only use the line to represent what is being repeated**
__
0.21212121 = 0.21
_
0.555555 = 0.5
__
0.2345454545 = 0.2345
Multiplying and Dividing Decimals
Multiplication:
0.34 x 2 = ?
0.34
x 2
-----------
0.68
Answer:
0.34 x 2 = 0.68
Division:
1 ÷ 8 = ?
0.1 2 5
8 ⟌ 1.0 0 0
-8 | |
---- V |
2 0 |
-1 6 |
----- V
4 0
-4 0
----------
0
Answer:
1 ÷ 8 = 0.125
0.125 = 12.5%
0.125 = 1/8
Adding and Subtracting Decimals
Adding:
1.24 + 1.35 = ?
1.24
+ 1.35
-------------
2.59
21.34 + 90.319 = ?
21.34
+ 90.319
---------------
111.659
Subtracting:
34.45 - 32.23 = ?
34.45
- 32.23
---------------
2.22
12.338 - 8.23 = ?
12.338
- 08.230
---------------
4.108
Week Ten
Practice Problems
There was ¾ of a pie in the refrigerator. John ate 2/3 of the left over pie. How much pie did he eat?
- First start by drawing out 3/4 on paper.
- Then shade 2/3 of whats left of the pizza.
- It would be 3/6 still shaded.
Jim, Ken, Len, and Max have a bag of miniature candy bars from trick-or-treating together. Jim took ¼ of all the bars, and Ken and Len each took 1/3 of all the bars. Max got the remaining 4 bars. How many bars were in the bag originally? How many bars did Jim, Ken, and Len each get?
Jim: 1/4 = 3/12 = 12 bars
Ken: 1/3 = 4/12 = 16 bars
Len: 1/3 = 4/12 = 16 bars
Max: 4 bars = 1/12
Draw a 3 x 4 grid containing 12 squares inside of it.
Week Eight
Fractions
Fractions:
Meanings:
- Part-Whole
- Quotient
- Ratio
Models:
- Surface Area
- Length
- Sets (groups of things)
20 Students
13 girls
7 boys
Fractions:
Girls 13 Boys 7
------- = ----- --------- = ----
Whole 20 Whole 20
Not Fractions:
Boys 7 Girls 13
-------- = ---- ------- = ----
Girls 13 Boys 7
3/7 > 1/7
4/5 > 4/9
3/7 < 5/8
9/10 > 3/4
4/ 4 = 1
1.4./ 1.4 = 1
x/ x = 1
xy/ xy =1
Week Six
EXAM 1
Week Four
Multiplication and Division
Division
8 ÷ 4 -> ÷ Division Sign
8/2 -> / Division/ Fraction Bar
2 ⟌8 -> ⟌ The rinculum
Quotient
V
4
2⟌8 <- Dividend
^
Divisor
Standard Algorithm Place Value Explicit
1 4 6 1 4 6
4 ⟌5 8 5 4 ⟌5 8 5
- 4 | | - 4 0 0
------V | --------
1 8 | 1 8 5
- 16 | - 1 6 0
---------V --------
2 5 2 5
- 2 4 - 2 4
--------- ---------
1 <-- Remainder 1 <-- Remainder
Alternative Algorithm
167 Pokemon Cards
12 in each booster pack
How many Packs? 13 Packs
12 ⟌ 1 6 7
- 1 2 0 --> 10 packs
-----------
47
- 36 --> 3 packs
-------------
11
- Standard Algorithm 2. Place Value 3. Expanded Notation
2
^ 19 19
19 x 13 x 13
x 13 ---------- ---------
---------- 3 x 9 = 27 -->20 10 + 9
5 7 3 x 10 = 30 10 + 3
+ 1 9 0 10 x 9 = 90 ----------
---------- + 10 x 10 = 100 110 + 7
2 4 7 --------------------- -----------
2 4 7 100 + 90 + 0
200 + 40 + 7
------------------
2 4 7
Week Two
Expanded Notation
Expanded Notation:
285 = 2 hundreds + 8 tens + 5 ones.
= 200 + 80 + 5
= (2 x 100) + (8 x 10) + (5 x 1)
= (2 x 10^2) + (8x10^1) + (5 x 10^0)
Note: When moving from left to right, the exponent must decrease by -1.
(Numbers to the power of 0 always equal 1)
For expanded notation, we are going to use the number 1342 with a base of 5.
13425
13425 = (1 x 5^3) + (3 x 5^2) + (4 x 5^1) + (2 x 5^0)
= (1 x 125) + (3 x 25) + (4 x 5) + (2 x 1)
= 125 + 75 + 20 + 2
= 222
2123 = (2 x 3^2) + (1 x 3^1) + (2 x 3^0)
= (2 x 9) + (1 x 3) + (2 x 1)
= 18 + 3 + 2
= 23
Numeration Systems
Base-10 (Decimal)
Using the number, 357.35, lets break down what each value represents.
Decimal
10's Point 1/100
V V V
3 5 7 . 3 5
^ ^ ^
100's 1's 1/10
<–––––––– –––––––––>
x10 ÷10
Base-10:
Ones - 10^0
Tens - 10^1
Hundreds - 10^2
Thousands - 10^3
When in base form, no value can exceed the number of the base. For example,
In base-10 there are 10 numeric digits:
0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Therefore, any value in base-form cannot be larger than 9.
So in base-5, the digits are 0, 1, 2, 3, and 4.
And again but in base-3, 0, 1, and 2.