arabera roberta nader 8 years ago
331
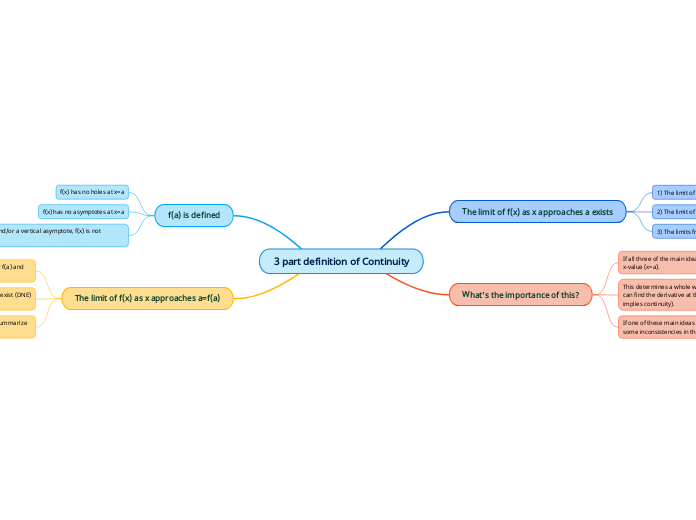
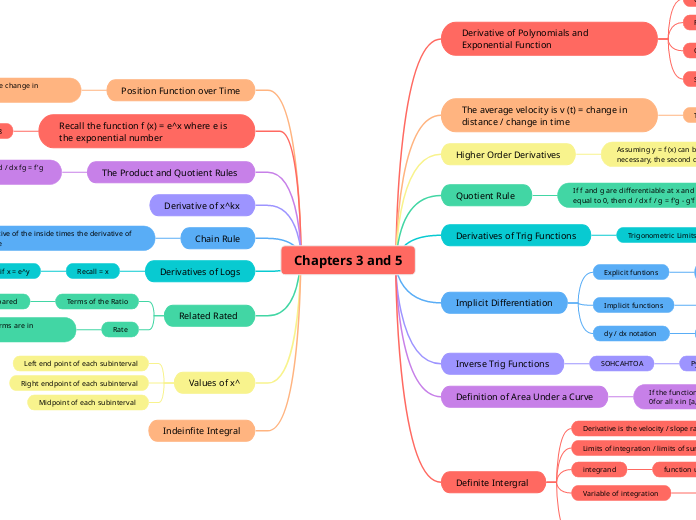
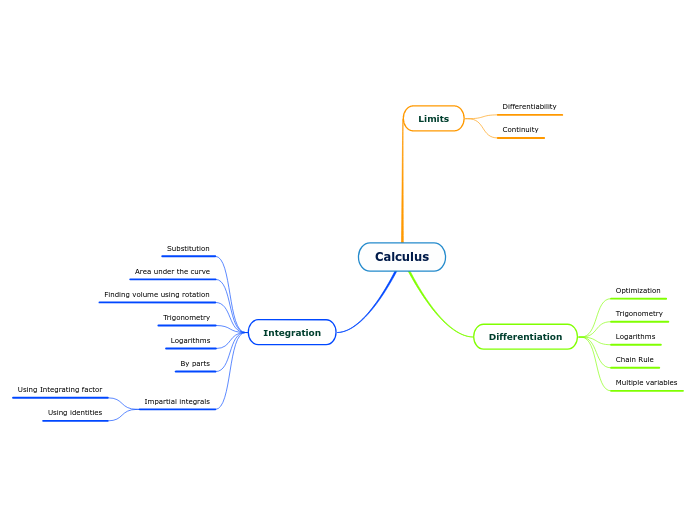
Limits Roberta Náder
Analyzing limits involves several methods including numerical and algebraic approaches. Numerically, one can determine limits by examining a table of values to see how a function behaves as it approaches a specific point.