Lineer Cebir
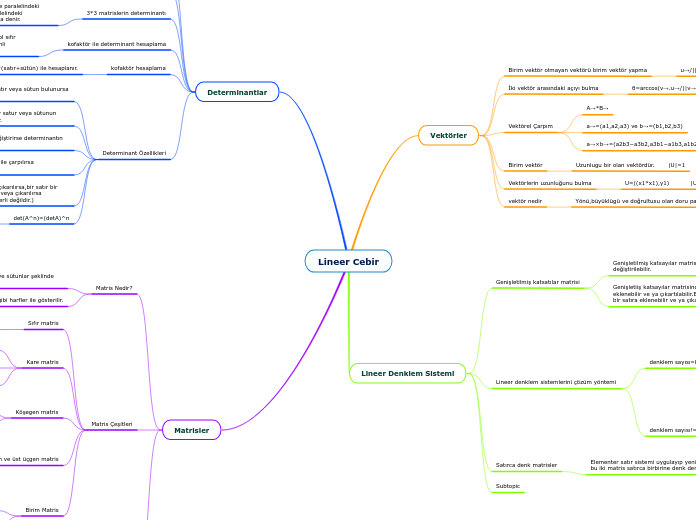
Matrisler
Matrislerde dört işlem
Matrislerde çarpma
İlk matrisin sütün sayısı=2. matrisin satır sayısı
Matrislerde çıkarma
Aynı satır ve sütunların çıkarılmasıyla elde edilir.
Matrislerde toplama
Aynı satır ve sütunların toplanmasıyla elde edilir.
Matris Çeşitleri
Birim Matris
Kre ve Köşegen matrislerdir.
Köşedeki elemanlar bir ve kalan elemanlar sıfır olan matrislerdir.
Alt üçgen ve üst üçgen matris
Üst üçgen
köşegenin üstünde sayılar ve altında sıfırlar olan matrislere alt üçgen denir.
Alt Üçgen
köşegenin altında sayılar ve üstünde sıfırlar olan matrislere alt üçgen denir.
Köşegen matris
Köşegenleri dışındaki tüm elemanları sıfır olan matrislerdir.
Bir kare matristir.Sadece kare matrislerde köşegen bulunur.
Kare matris
NOT=Sadece kare matrislerin tersi alınabilir.
NOT=Sadece kare matrislerin determinantı vardır.
Satır ve sütun sayıları eşit olan matrislere denir.
Sıfır matris
Bütün satıları ve sütunları sıfır olan sayılara sıfır matris denir.
Matris Nedir?
Matrisler A,B,C gibi harfler ile gösterilir.
Köşeli parantezin içine sayıların satırlar ve sütunlar şeklinde yazılmasıdır.
Determinantlar
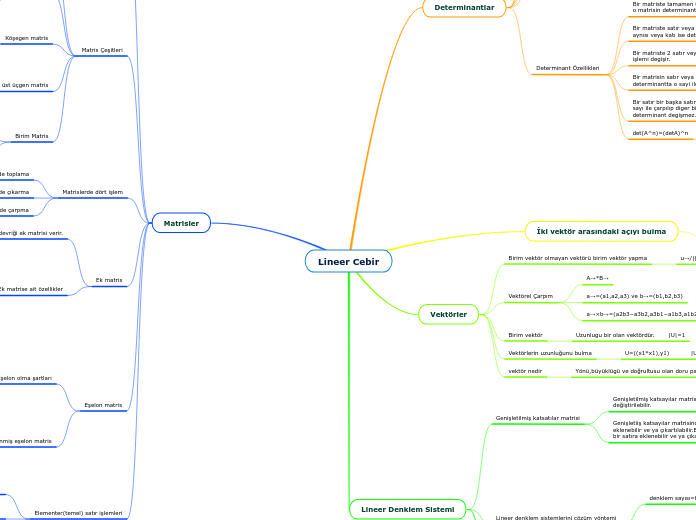
Determinant Özellikleri
det(A^n)=(detA)^n
det(A^T)=detA
det(A^-1)=1/detA
Bir satır bir başka satıra eklenir veya çıkarılırsa,bir satır bir sayı ile çarpılıp diger bir satıra eklenir veya çıkarılırsa determinant degişmez.(sütun için geçerli değildir.)
Bir matrisin satır veya sütunu bir sayı ile çarpılırsa determinantta o sayi ile çarpılmalıdır.
Bir matrıste 2 satır veya sütun yer değiştirirse determinantın işlemi degişir.
Bir matriste satır veya sütun başka bir satur veya sütunun aynısı veya katı ise determinant 0 olur.
Bir matriste tamamen 0 dan oluşan satır veya sütun bulunursa o matrisin determinantı sıfır olur.
kofaktör hesaplama
(-1)^(satır+sütün) ile hesaplanır.
kofaktör ile determinant hesaplama
matriste istenilen satır ve sütün seçilir(genellikle bol sıfır olanlar),hangi satır veya hangi sütun seçildiği önemli değildir,hepsınde aynı sonuç çıkar.
3*3 matrislerin determinantı
3*3 matrislerin determinantı asıl köşegen ve paralelindeki köşegenleri toplayıp,yedek köşegen ve paralelindeki köşegenleri toplayıp birbirinden çıkarılmasına denir.
2*2 matrislerin determinantı
2*2 matrisin determinantı (asıl köşegen*yedek köşegen) denir.
1*1 matrislerin determinantı
1*1 matrisin determinantı kendisine eşitiir.
Lineer Denklem Sistemi
Satırca denk matrisler
Elementer satır sistemi uygulayıp yeni matris elde ettiğimizde bu iki matris satırca birbirine denk denir.
Lineer denklem sistemlerini çözüm yöntemi
denklem sayısı!=bilinmeye sayısı
satırca indirgenmiş eş alan form
Satırca eş alan form yoluyla
denklem sayısı=bilinmeyen sayısı
Subtopic
Satırcaeş alan form
Cramer metodu
Gauss jordan yok etme metodu
Gauss yok etme metodu
Genişletilmiş katsatılar matrisi
Genişletiiş katsayılar matrisinde bir sayı diğer bir sayıya eklenebilir ve ya çıkartılabilir.Bir satır bir sayı ile çarpılıp diğer bir satıra eklenebilir ve ya çıkartılabilir.
Genişletilmiş katsayılar matrisi istenildiğinde iki satırın yeri değiştirilebilir.
Vektörler
vektör nedir
Yönü,büyüklügü ve doğrultusu olan doru parçalarıdır.
Vektörlerin uzunluğunu bulma
U=((x1*x1),y1) |U|=√(x1*x1)+(*y1y1)
Birim vektör
Uzunlugu bir olan vektördür. |U|=1
Vektörel Çarpım
a→×b→=(a2b3−a3b2,a3b1−a1b3,a1b2−a2b1)
a→=(a1,a2,a3) ve b→=(b1,b2,b3)
A→*B→
İki vektör arasındaki açıyı bulma
θ=arccos(v→.u→/||v→||.||u→||
Birim vektör olmayan vektörü birim vektör yapma
u→/||u→||