arabera Gabriel Rosales Dominguez 3 years ago
515
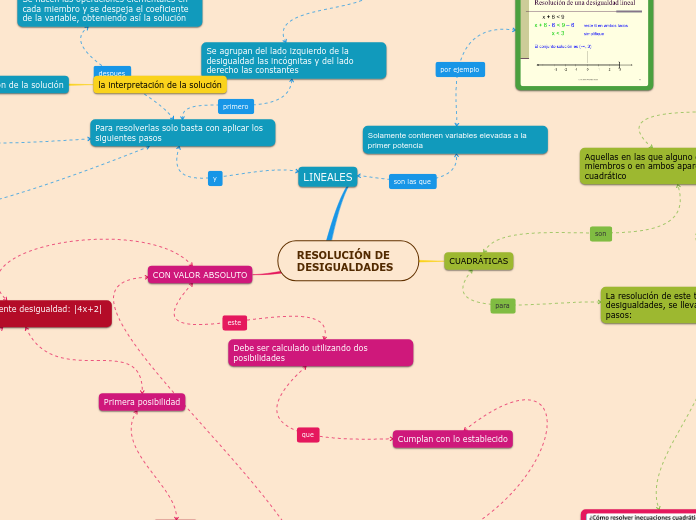
Mapa Mental - Desigualdades
Las desigualdades pueden ser lineales, cuadráticas o con valor absoluto y se resuelven agrupando términos y despejando variables. Para una desigualdad absoluta como |4x+2| > 6, se consideran dos casos: