arabera Matheus Raynal 4 years ago
331
Organigrama
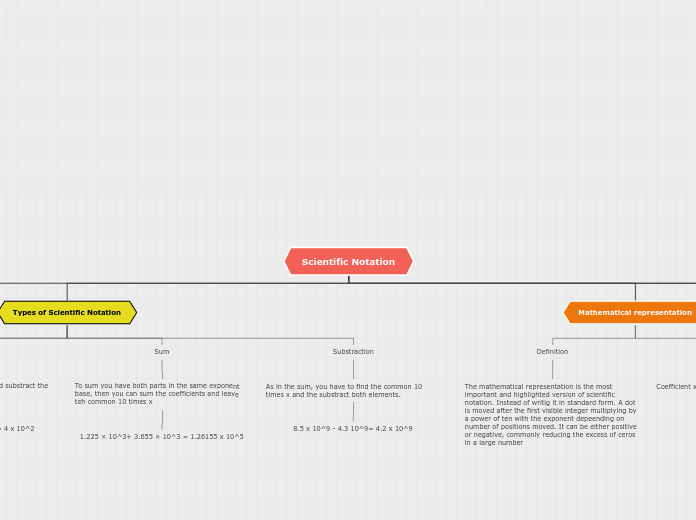
Scientific notation is a method used to express very large or very small numbers in a more compact and manageable form. By leveraging powers of ten, it simplifies calculations and reduces the number of characters needed to represent a number.