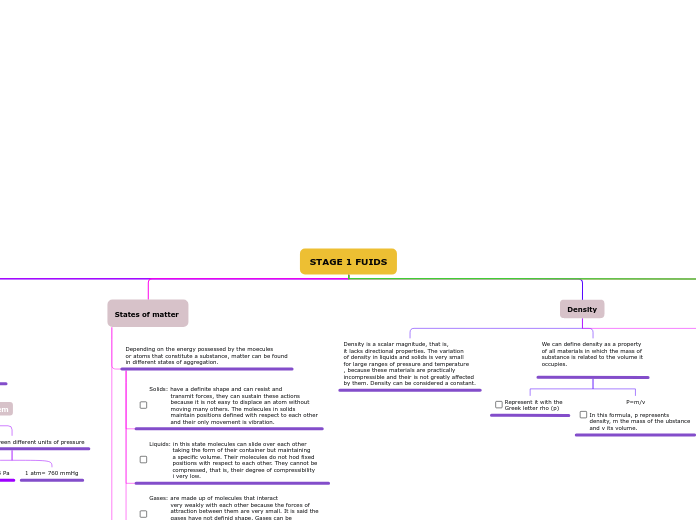
STAGE 1 FUIDS
Properties of liquids
Understanding the behavior of liquids
in common situations
At first glance, it seems that the volume in container A would
exert a greater pressure on the bottom than, for example, container C. If this were true, such pressure would force the liquid to rise higher in container C. When the containers are filled with a liquid, the levels are shown to be equal. For example, the area of the liquid at the bottom container C;
therefore, the liquid will exert a greater force on the bottom
of container A than in C. But the greatest force is applied
over a large area so that the pressure is the same in both vessels.
This principle is known as the principle of
communicating vessels.
Archimedes Principle
E=pgV
The latter equation represents the force exerted
by the fluid upward on the cylinder, Wich is called
thrust force (E)
If we write the equation as follows:
E=pVg
we observe that the product (pV) represents
the mass of the fluid (m), and the mass multiplied
by (g) is the weight of the fluid. Principle can be stated
as follows: A submerged body receives a thrust force equal
to the weight of the fluid that displaces the body.
Fluids exert pressure against their own particles
and against the walls containing them. If a solid body
is submerged in fluid, it will receive the fluid pressure.
Presure and fluids
To formulate the relatonship of the
dependence of pressure on the depth
of liquids.
Solids have a resistance to penetrating or cutting forces,
and besides resist stress and compression. Fluids do not
resist tensile stress or cutting, but they can with stand compression forces when located within a closed space.
fluids exert forces on the surfaces with which they are in contact. These forces can be calculated if we know the value of the pressure exerted by the fluid and the area of the given surface. That pressure is defined as force per unit area.
To determine what factors affect the
pressure inside a fluid.
We must analyze the pressure that it exerts on a surface
depending on the weight of the same column of fluid.
Density
Measuring scales
cgs system
p(=)g/cm3
International system
p(=)kg/m3
We can define density as a property
of all materials in which the mass of
substance is related to the volume it
occupies.
P=m/v
In this formula, p represents
density, m the mass of the ubstance
and v its volume.
Represent it with the
Greek letter rho (p)
Density is a scalar magnitude, that is,
it lacks directional properties. The variation
of density in liquids and solids is very small
for large ranges of pressure and temperature
, because these materials are practically
incompressible and their is not greatly affected
by them. Density can be considered a constant.
States of matter
Another state of aggregation is plasma
Metacognitivas
Plasma: is a gas whose atoms are ionized, wich means
thet some or all of its atoms that have lost
electrons, becoming conductors of electricity,
unlike gases, which are not conductors.
Depending on the energy possessed by the moecules
or atoms that constitute a substance, matter can be found
in different states of aggregation.
Gases: are made up of molecules that interact
very weakly with each other because the forces of
attraction between them are very small. It is said the
gases have not definid shape. Gases can be
compressed because the space between their
molecules is large.
Liquids: in this state molecules can slide over each other
taking the form of their container but maintaining
a specific volume. Their molecules do not hod fixed
positions with respect to each other. They cannot be
compressed, that is, their degree of compressibility
i very low.
Solids: have a definite shape and can resist and
transmit forces, they can sustain these actions
because it is not easy to displace an atom without
moving many others. The molecules in solids
maintain positions defined with respect to each other
and their only movement is vibration.
Concept of pressure
A fundamental concept of physics known as pressure.
If F is the magnitude of a perpendicular force exerted
on a gven area A, the the pressure P is defined as the
force applied per unit of area:
P=F/A
Pressure units in the international system
Conversion rates between different units of pressure
1 atm= 760 mmHg
1 atm= 1.013x10´5 Pa
P(=)N/m2
is commonly know as Pascal (Pa)
Other commonly used units of pressure
are: pounds pers square inch (Ib/in2), or psi,
is widely used to measure air pressure in car tires;
miimeters of mercury; atmosphere (atm), and bar,
generally used to refer to atmospheric pressure.
Pascals Principle
Pascal Principle applies to many devices that
are used in daily life and in industry. Was discovered by
Blaise Pascal, French mathematician, physicist, and theologian, and proven experimentally.
Analyze the expression of the pressure inside a volume
of liquid:
P2-P1=pgh
In the above formula we can see that the difference between
the pressures only depends on the density of the liquid,
the acceleration of gravity and height.
From the above it follows that:
PB-PA=pgh
If for some reason the pressure at A increases
by a value P, the pressure at B must be increased by a value equal to P.
(PB+P)--(PA+P)=pgh
Atmospheric pressure
When pressure is measured with respect to
atmospheric pressure, it is called gauge pressure.
When you want to calculate the pressureat a
certain depth within a liquid, considering the atmospheric
pressure, it is posible to use teh above expression, replacing
the term of the gauge pressure with that of the hydrostaic pressure.
Pabs=Patm+pgh
When the total pressure is measured, considering
the atmospheric pressure, it is said that the absolute
pressure is taken.
Pabs=Patm+Pman
Inside the tire there are 25 or 30
psi above the atmospheric pressure
Pman=Pabs--Patm
Earth is surrounded by a layer of gas, wich we call the atmosphere. It is actually a mixture of gases but they behaves as one, which we call air. The composition of the atmosphere is 78% nitrogen, 20% oxygen,
1% argon, and the rest is made up of gases
such as carbon, neon, helium, water vapor,
and so on.
Calculation of atmosphere
Normal atmospheric pressure, at sea level, is equal
to 760 milimeters of mercury. equals 1013 mbar, 14.7
psi or 1.013x10´5 Pa.