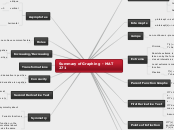
Summary of Graphing - MAT 271
Symmetry
f(-x) = -f(x) => the function is and ODD function => the graph passes through (0,0) and is symmetrical about the origin (turn graph upside down = looks the same
Periodic functions
f(-x) = f(x) => f is an EVEN function => symmetry about the y-axis
Second Derivative Test
If f'(c)=0 and f''(c)>0, then f has a local minimum at c
If f'(c) = 0 and f''(c)<0, then f has a local maximum at c
Concavity
Concave down if second derivative is negative
Concave up if second derivative is positive
Transformations
Increasing/Decreasing
Increasing where first derivative is positive
Decreasing where first derivative is negative
Holes
Occur where num. and denom. have common factors
Asymptotes
horizontal
Rational Function - compare degrees of num. and denom.
If same - ha is y = ratio of leading coefficients
Calculus - evaluate the limit as x approaches + or - infinity
If num. degree is less than the denom. - ha is y = 0
vertical
Rational function - where denominator = 0
oblique
If num. degree is greater than the denom. - found by long division
If the num. degree is 1 more than denom. - it's called a slant asymptote - found by long division
Vertical Line Test
To verify a function has been drawn
Plot a Few Points
Points of Inflection
If f''(c) exists and f'' changes sign at c, then we have an inflection point at c. Inflection point is (c, f(c)). If f''(c) is an inflection point, then f''(c) = 0.
First Derivative Test
Assumes c is a critical number and f is continuous
If f' does not change sign at c, then f has no local max or min at c.
If f' cjanges from - to + at c, then f has a local min at c.
If f' changes from + to - at c, then f has a local max at c.
Parent Function Graphs
Trig functions - period/amplitude, etc.
Extrema
Maxima
f'(c) = 0, second derivatie is negative OR f'(c) = 0 and f' changes from + to - at c. The maximum value is f(c).
Local extrema is max/min on some interval of the function
Absolute extrema is the largest or smallest value taken on by the function (Consider endpoints of closed intervals as well as all local extrema)
Minima
f'(c) = 0, second derivative is positive OR f'(c) = 0 and f' changes from - to + at c . The minimum value is f(c)
Jumps
non-continuous - piece-wise functions
Intercepts
x-intercept(s) => set y = 0
y-intercept => set x = 0
Domain of the function
Denominator can not equal 0
You can only take a logarithm of a positive number
Domain info can give you the start or end of a graph
Real life restrictions (no negative distances, time, etc.)
You can only take even roots of non-negative numbers