Функції

Lisää tämän kaltaisia

Криві

luonut Антоніна Мельник

План организации

luonut Светлана Черняева

Статистические гипотезы,критерии согласия, парметрические критерии

luonut Юля Королёва

Sample Mind Map

luonut Таня Сидоренко

Функції

Функцією з областю визначення D називають залежність, згідно з якою кожному числу х із множини D відповідає за деяким правилом єдине число у із множини Е.

   Змінну х називають незалежною змінною або аргументом функції, а змінну у – залежною змінною або функцією.

Способи задання

Існує чотири основних способи задання функції:

1. Аналітичний спосіб
2. Табличний спосіб
3. Графічний спосіб
4. Словесний спосіб

Графічний

При  графічному способі задання  зображають графік функції 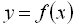  в системі координат х0у.  Графіком функції  називається зображення на координатній площині множини упорядкованих пар  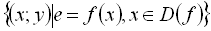. Кожній упорядкованій парі дійсних чисел  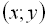 можна поставити у відповідність точку на площині. Для цього на площині зображають прямокутну (декар-тову) систему координат х0у (рис. 1). Прямі 0х і 0y взаємно перпендикулярні, 0 – точка пере-тину цих прямих. 0х – вісь абс-цис, 0y – вісь ординат, 0 – початок координат. На кожній з осей 0х і 0y вибирають позитив-ний напрям відліку (на осі 0х – зліва направо, на осі 0y – знизу угору). Вибирають також одиницю виміру (масштаб). Кожна точка  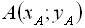 на корди-натній площині має дві коор-динати:  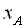 – абсцису,  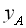 – ординату . Таким чином,  графік функції  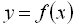 – множина точок координатної площини х0у, абсциси яких є значеннями аргументу  х , а ординати – відповідні значення функції  у .

Аналітичний

При даному способі задання функція задається за допомогою формули 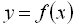 , де 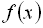  – деякий вираз із змінною  х .

Табличний

Табличний спосіб задання функції  полягає в тому, що відповідність між елементами множин 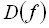  і 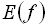  задається у формі таблиці. При цьому способі наводиться таблиця, що вказує значення функції  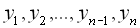 для наявних в таблиці значень аргументу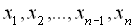 

Словесний(описовий)

При словесному способі задання функції закон, за яким значення функції відповідають значенням аргументу, формулюється словесно. Так, наприклад, розмір прибуткового податку є функцією заробітної плати платника податків.

Квадратична

y=ax2+bx+c,

a (a≠0), b, c — числа.

Графік — парабола.

Послідовність кроків при побудові графіка квадратичної функції:

1. визначити напрям віток параболи;
2. знайти координати вершини параболи (m;n)(m;n);
3. знайти ординату перетину з віссю OyOy;
4. відкласти точку, симетричну їй відносно прямої x=mx=m;
5. знайти абсциси точок перетину з віссю OxOx;
6. за потреби, скласти таблицю значень для визначення ще декількох точок.

Квадратичною називають функцію виду y=ax^2+bx+c, де а, b, с – дійсні числа, причому а≠0.

Область визначення квадратичної функції - вся числова пряма.

При  функція не є парною і не є непарною. При  квадратична функція - парна.

Квадратична функція неперервна  і диференційовна на всій області визначення.

Функція має єдину критичну точку 

Область зміни функції: при  - безліч значень функції ; при  - безліч значень функції 

Лінійна

y=k⋅x+l,

k, l — числа. Графік — пряма, що перетинає вісь абсцис у точці (−lk; 0), ординат — (0; l).

Графіком лінійної функції є пряма, тому для побудови графіка досить побудувати таблицю для двох значень аргументу і функції.

Якщо числа k і b не дорівнюють нулю, то пряма перетинає вісь абсцис і вісь ординат.

Якщо k ≠ 0, аb = 0, то пряма проходить через початок координат.

Якщо k = 0, аb ≠ 0, то пряма проходить паралельно осі абсцис і перетинає вісь ординат у точці b.

Область визначення лінійної функції – вся числова пряма.

Область значень лінійної функції – вся числова пряма.

При k, більшому за нуль, функція є зростаючою.

При k, меншому від нуля, функція є спадною.

Функція виду y=kx+b, де k, b – деякі числа, х – незалежна змінна, називається лінійною. Характерною особливістю лінійної функції є пропорційна зміна значення функції при зміні аргументу.

Обернена пропорційність

Функцію, задану формулою y =kх , де х — незалежна змінна, k ≠ 0 — дане число, називають оберненою пропорційністю.

Область визначення функції y =k/x — множина всіх чисел, крім 0. Графік функції y =k/x (k ≠ 0) — гіпербола, симетрична відносно початку координат. Коли k > 0, вітки гіперболи розміщені в I і III координатних кутах, коли k < 0 — у II і IV.

Пряма пропорційність

y=k⋅x,

k — число. Графік — пряма, що проходить через початок координат під кутом до осі абсцис

tgα=k.

Для визначення проміжків монотонності функції виберемо два довільних значення аргументу х₁ і х₂ таких, що х₁>х₂. Якщо k>0, то kх₁>kх₂, тобто f(х₁)>f(х₂). Це означає, що при k>0 функція прямої пропорційності зростає на всій області визначення. Якщо k<0, то із нерівності х₁>х₂ випливає kх₁<kх₂, тобто f(х₁)<f(х₂). Це означає, що при k<0 функція прямої пропорційності спадає на всій області визначення.

Для того, щоб визначити парною чи непарною є ця функція, відповідно до означення непарних функцій маємо: f(-х)=k(-x)= -kx= -f(х), тобто справедлива рівність f(-х)= -f(х). Це означає, що функція у=kх є непарною, а її графік повинен бути симетричним відносно початку координат.

Функція, яку можна задати формулою виду у = kх, де х – аргумент, k – число (k ≠ 0), називається прямою пропорційністю.

Пряма пропорційність - окремий випадок лінійної функції)

Степенева

Якщо показник степеня n— натуральне число, то степенева функція задається формулою y=x

Якщо показник степеня — ціле від'ємне число, то степенева функція задається формулою y=x^(-n).

Графік

Властивості

При знаходженні області визначення слід пам’ятати, якщо функція має вигляд y=xp, то:

• якщо α – натуральне число, то D(y)=R;
• якщо α – ціле від’ємне число або нуль, то D(y)=(−∞;0)∪(0;+∞);
• якщо α – додатне не ціле число, то D(y)=[0;+∞);
• якщо α – від’ємне не ціле число, то D(y)=(0;+∞).

Означення

Функція вигляду 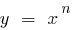, де n — будь-яке дійсне число, називається степеневою функцією.
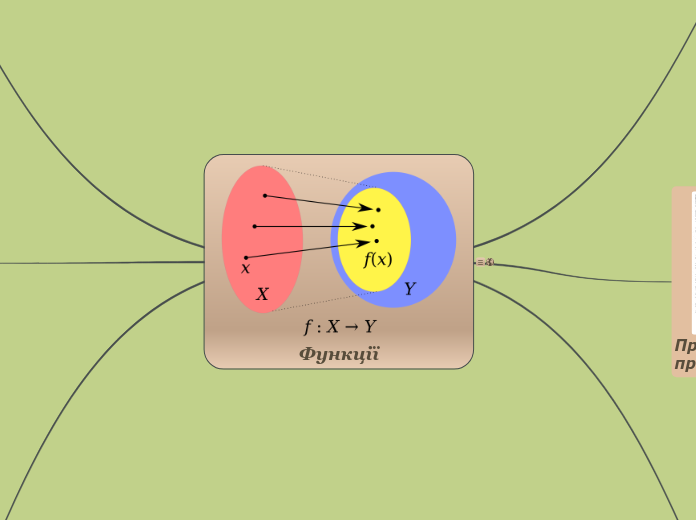
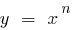