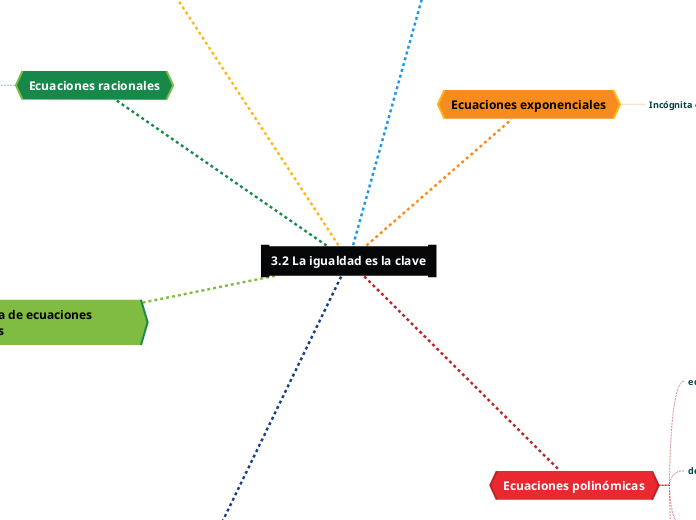
3.2 La igualdad es la clave
Tips:
- Cover letters should be one page long and divided into three to four paragraphs.
- In general, a relevant and short cover letter is best. Three paragraphs tops. Your go-to word count shouldn’t exceed 300 words.
- When sending a cover letter via email, include your name and the job you're applying for in the subject line of the message.
Sistemas no lineales
In the second paragraph you should show why you are the perfect fit.
sistemas de ecuaciones exponenciales y logarítmicas
realizamos los cambios de variable
a^m = s b^n =t
y resolvemos el sistema lineal obtenido.
Hallamos las soluciones deshaciendo los cambios devariables
sistema cuadrático
You can also highlight your achieved results at the job.
Se pueden resolver por reducción o por sustitución
PASO A SEGUIR
Resolvemos el sistema por sustitución despejando la incógnita y de la ecuación lineal y sustituyendo en la ecuación cuadrática.
Es tan simple como despejar una incognita y sustituir el valor obtenido en la otra ecuación
Subtópico
tipos
You have the opportunity to express your qualifications for the job in more detail than on your resume.
Sistema de ecuaciones lineales
The third paragraph should prove that you’ll fit in and why the company is the perfect fit for you!
métodos de resolución
Show that your experience and knowledge will let you succeed with the project and benefit the company.
Igualación: Se despeja la misma incógnita en ambas ecuaciones y se igualan las
expresiones obtenidas.
Sustitución: Se despeja una de las incógnitas en una de las ecuaciones y se sustituye la expresión obtenida en la otra ecuación.
Reducción:Se multiplican las ecuaciones por los números adecuados para que, al sumarlas, se elimine una incógnita.
tipos
Show that you did your research and know something about the company, perhaps an upcoming project, etc.
Sistema compatible indeterminado
Sistema incompatible
(no puedo poner foto porque necesito "premium")
Sistema compatible determinado
Ecuaciones racionales
The best cover letter ending is by providing value.
Tell the hiring manager that you look forward to meeting them in person and discuss.
incógnita en denominador
1. Eliminamos los denominadores.
2. Resolvemos la ecuación polinómica obtenida.
3. Descartamos las soluciones que anulen algún denominador de la ecuación inicial.
Ecuaciones irracionales
A cover letter is a professional correspondence, so you should always use formal closing!
Best wishes
Cheers
Eagerly waiting for a response
Warm regards
Warmest regards
Warmly
Have a great day
Yours faithfully
Abbreviations
Emojis
Con raíces cuadradas
1. Aisiamos la raiz en un miembro de la ecuacion.
2. Elevamos al cuadrado ambos miembros, operamos y resolvemos la ecuación obtenida.
3. Comprobamos las soluciones obtenidas en la ecuación original.
Ecuaciones polinómicas
The header of every professional cover letter should include your contact information, employer's contact information.
mayores de 2° grado
1.° Extraemos xfactor común:
2.° Factorizamos el polinomio
3. SI el cociente no tiene raíces enteras, lo factorizamos. Luego resolvemos la ecuación de segundo grado.
de 2° grado
Optionally you can add
Para resolverlas tenemos que aprender las identidades notables
Despues resolvemos como una ecuación normal, siguiendo la jerarquía y demás
de 1° grado
1. Eliminamos los denominadores
2. Eliminamos los paréntesis
3. Agrupamos términos y simplificamos
ecuaciones bicuadradas
PASOS A SEGUIR
1. Realizamos el cambio de variable x2 = z, reescribimos la ecuación y la resolvemos (fórmula de ecuación de grado 2)
2. Deshacemos el cambio de variable y resolvemos
Ecuaciones exponenciales
Incógnita en el exponente
Es crucial saber las propiedades exponenciales:
1. a^m = a^n -> m = n
2. a^x = z
3. a^m = a^n -> log a^m = log b^n
Ecuaciones logarítmicas
The post script is a great hack to draw the hiring manager's attention one last time!
You should use the P.S. to tell something impressive about your career.
Con logarítmos
Los sistemas de ecuaciones exponenciales y logarítmicas suelen resolverse por cambio de variable.
1. Escribimos cada miembro de la ecuación con un solo logaíttmo.
2. Aplicamos una propiedad logaritmica para obtener una ecuación polinómica y la resolvemos.
3. Comprobamos la validez de las soluciones verificando que los logaritmos están definidos.
Es crucial saber las propiedades logarítmicas:
1. Log (b.c)= Log b + Log c
2. Log (b:c)=Log b - Log.c