jonka alejandra samboni 2 vuotta sitten
153
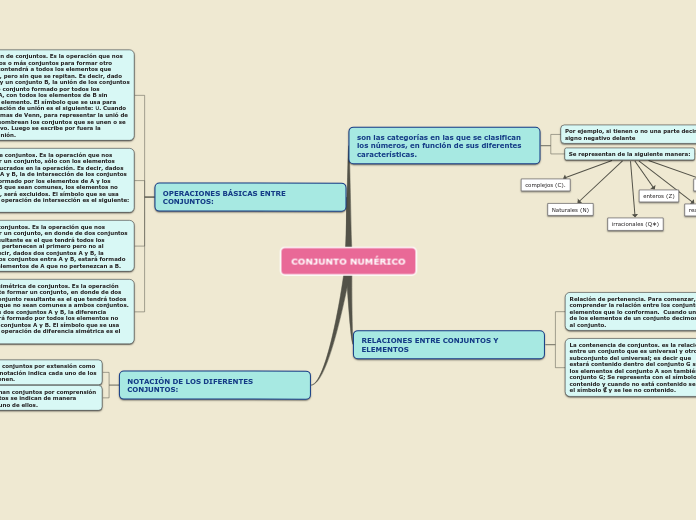
CONJUNTO NUMÉRICO
Los conjuntos numéricos se pueden representar de diversas maneras, siendo por comprensión y por extensión las más comunes. La comprensión describe los elementos de manera general, mientras que la extensión enumera cada uno de los elementos del conjunto.