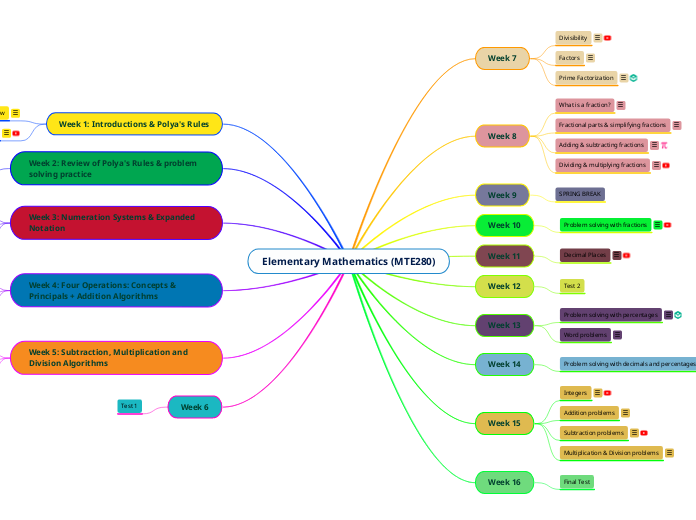
Elementary Mathematics (MTE280)
Week 6
Test 1
Week 5: Subtraction, Multiplication and Division Algorithms
Division Algorithms
8 = dividend
_________ 2 = divisor
2 l 8 the answer = qoutient
8 / 2 = 4 R0
Division Algorithms
- Standard
- Place Value
- Alternate Algorithm
*** Refer to notebook on how to do these.
Multiplication Algorithms
Multiplication Algorithms
- Standard
- Place Value
- Lattice
*** Refer to notebook on how to do these.
Subtraction Algorithms
7 minuend
-3 subtrahend
----
4 difference
Subtraction Algorithms
- American Standard
- European/Mexican
- Reverse Indian
- Left-to-Right
- Integer Subtraction
- Expanded Notation
*** Refer to notebook on how to do these.
Week 4: Four Operations: Concepts & Principals + Addition Algorithms
Multiplication
Multiplication (aka groups of things)
- Identity property: a, a x 1 = a
- Commutative property: a, b: a x b = b x a
- Associative property: a, b, c: (a x b) x c = a x (b x c)
- Zero property: a, a x 0 = 0
- Distributive property: a x (b x c) = (a x b) + (a x c)
Arrays
---------} #2
________________
l 0 0 0 0 0 0 0 l l
l 0 0 0 0 0 0 0 l l
l 0 0 0 0 0 0 0 l l #1 3 x 7 = 0
l 0 0 0 0 0 0 0 l l
l 0 0 0 0 0 0 0. l l
l 0 0 0 0 0 0 0 l V
________________
Subtraction
Subtraction
- Take away: 4-1=3
- Comparison (?): 4-1=3 - I read 4 books and she read 3 books. How many more books did I read than her? (3)
- Missing addend (?): 4+( )=7 ----} 7-(4)=( ) - Ivan has 4 cookies, mom gave her more and now she had 7. How many cookies did mom give Ivan?
Subtraction Algorithms
-
Addition
Addition (aka putting things together)
- Identity property: for any number a, a+0=a (when you add zero, a number's identity does not change)
- Commutative property (aka "order" property): for any two numbers a & b, a+b=b+a (the order you add the numbers does not matter)
- Associative property (aka "grouping" property): for number a, b, c: (a+b)+c=a+(b+c) - the way you group any numbers does not matter.
Addition Algorithms
- American Standard - should be the last step
- Partial Sums - emphasizes place value, right to left
- Partial Sums (b) - adds them by actual place value, right to left
- Left-to-Right - emphasis on place value, kids read left to right
- Expanded Notation - emphasis on place value, separate by values, the BEST way to start teaching addition
- Lattice - just for fun. Not in traditional textbooks
Week 3: Numeration Systems & Expanded Notation
Base-5 System
BASE-5 SYSTEM
Australians use the Base-5 System because there are 5 fingers on a hand
The place values differ from Base-10
Digits used: 0,1, 2, 3, 4, 10(base 5), 11(base 5), 12(base 5), 13(base 5), 14(base 5), 20(base 5)
How to convert Base-5 to Base-10:
232 (base 5) = (2x25)+(3x5)+(2x1)
232 (base 5) = (2x5^2)+(3x5^1)+(2x5^0)
232 (base 5) = 50 + 15 + 2
232 (base 5) = 67
The video shows a much faster, straight forward way to convert without showing as much work. But, it shows what the thinking process should be while converting
Expanded Notation
Expanded Notation
the simple definition is to break down or expand numbers.
For example in Base-10:
375 = 300 + 70 + 5
375 = (3x100)+(7x10)+(5x1)
375 = (3x10^2)+(7x10^1)+(5x10^0)
Base-10 System
BASE-10 SYSTEM
In the US, we use the Base-10 system (also referred to as a decimal or positional system)
Numbers always relate to each other on a 1-10 relationship
The spot where a number is placed indicates the number's value
When you move to the left, the number gets bigger by 10 times
When you move to the right, the number gets smaller by 10 times
For example:
375
- the 5 is considered the "ones-units"
- the 7 is considered the "tens-units"
- the 3 is considered the "hundreds-units"
The same applies for different units such as decimals, money, miles, etc.
Week 2: Review of Polya's Rules & problem solving practice
Review of Poyla's 4-step problem solving process
POLYA'S RULES
Step 1: Understand the problem.
Step 2: Devise a plan (translate).
Step 3: Carry out the plan (solve).
Step 4: Look back (check and interpret).
This week we solved more problems while applying this method. The biggest thing I took away from this week is that MULTIPLICATION tables are the key to solving a lot of problems!
Our professor had us start off as doing problems the "hard" way, then at the end of class revealed the "easy" way. It was very helpful to start our problem solving without having the easier method so that we could understand how things are broken down and how different students could interpret problems differently.
Week 1: Introductions & Polya's Rules
Polya's 4-step problem solving process
POLYA'S RULES
Step 1: Understand the problem.
Step 2: Devise a plan (translate).
Step 3: Carry out the plan (solve).
Step 4: Look back (check and interpret).
We solved a few problems in class using these steps. Multiple students would go up to the board and write out how they solved problems to show different ways of interpreting the problems.
Introduction to the class / syllabus review
INTRODUCTION
The syllabus includes just about all the information for this course that I could ever need. It includes contact information, policies, assignments, and information about the course itself.
The syllabus can be found on canvas.
Week 16
Final Test
Week 15
Multiplication & Division problems
+3 x -2 = -6 (-)(-)(-)(-)(-)(-) **3 groups of -2
+6 / 2 = +3 (+)(+)(+)(+)(+)(+) ** 3 groups of 2 in 6
Subtraction problems
+5 - -1 = +4 (+)(+)(+)(+)(+) - (+) = (+)(+)(+)(+)
-5 - +1 = -6 (-)(-)(-)(-)(-) - (+)(-) = (-)(-)(-)(-)(-)(-) **cross out (+)
Addition problems
-5 + -1 = -6 (-)(-)(-)(-)(-) + (-) = (-)(-)(-)(-)(-)
-5 + +1 = -4 (-)(-)(-)(-)(-) + (+) = (-)(-)(-)(-) **cross out (+) & one (-) because it is a zero pair
Integers
Integers are positive and negative numbers.
-------l--------l------l-------l-------l-------l-------l-------l-------l-----
-4 -3 -2 -1 0 1 2 3 4
- Chip method: use two-colored tokens for probability, positive/negative numbers.
- red: negative (-)
- yellow: positive (+)
- (+) & (-) = "zero pair"
Example:
+5 + +1 = +6 (+)(+)(+)(+)(+) + (+) = (+)(+)(+)(+)(+)(+)
Week 14
Problem solving with decimals and percentages
- Use square method in order to solve the problems.
- Use long division
- Determine whether the answer is terminating or not.
Week 13
Word problems
Problem solving with percentages
Pay attention to the wording of a problem - it will tell you what you need to solve for.
- 9/25 students voted for Marina, what percentage voted for Marina?
25n/25 = 100 x 9/25
n = 100 x 9 / 25
36% of students voted for Marina
Week 12
Test 2
Week 11
Decimal Places
3 7 5 . 3 2
100's 10's ones 1/10 1/100
3/10 is 3 dimes
3/10 = 0.3 = 0.30
0.8 = 8/10 "eight tenths"
0.123 = "123 thousandths"
0.003 = three thousandths
72/100 = 0.72
31/1000 = 0.031
0.83 = 83/100
5/6 = 5 divided by 6 (do long division) = 0.83 (3 repeating)
Week 10
Problem solving with fractions
In order to successfully teach children how to problem solve with fractions, you HAVE to draw pictures!
Each fraction of a whole is equal in value.
Example:
If **** represents 2/7 of the whole, draw what the whole looks like.
** = 1/7
**** = 2/7
****** = 3/7
******** = 4/7
********** = 5/7
************ = 6/7
************** = 7/7
Week 9
SPRING BREAK
Week 8
Dividing & multiplying fractions
Multiplying fractions
- Multiply ACROSS
EX: 1/3 X 1/8 = 1/24
Dividing fractions
- Keep
- Change
- Flip
EX: 2/3 divided by 4/5
- Keep 2/3 the same
- Change division sign to multiplication sign
- Flip 4/5 to 5/4
- Solve
2/3 X 5/4 = 10/12
Adding & subtracting fractions
Adding fractions with common denominators:
1/4 + 2/4 = 3/4
2/5 +2/5 = 4/5
3/8 + 4/8 = 7/8
** add the numerators, don't change denominator.
Subtracting fractions with common denominators:
5/7 - 2/7 = 3/7
9/10 - 1/10 = 8/10
** subtract the numerators, don't change denominator.
If the denominators aren't the same?
- Find a common multiple for the denominators.
- Multiply the fraction by one
EX:
1/4 + 1/6
- Common multiple for denominators: 12
- Figure out what each denominator needs to be multiplied by in order to become 12
- Multiply 1/4 by 3/3 (1)
- Multiply 1/6 by 2/2
ANSWER: 3/12 + 2/12 = 5/12
Fractional parts & simplifying fractions
Fractional parts are equivalent parts.
- When the numerator and denominator are the same, it equals one.
- EX: 6/6 = 1
- The more pieces you put, the smaller the pieces get.
To simplify fractions, you need to:
- Find a common factor
- Divide by 1
** The bigger the common factor, the less steps you will have to simplify a fraction
EX:
25/100
- Find a common factor: the greatest common factor is 25
- Divide by 1: DIVIDE 25/100 by 25/25
ANSWER: 1/4
What is a fraction?
Models:
- Set (group of things)
Fraction:
- Part-Whole
- Quotient
- Ratio
Week 7
Prime Factorization
All prime numbers 1-60:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59
Best ways to factor:
Use the factorization tree OR list method to find the Greatest Common Factor (GCF) and Least Common Multiple (LCM)
Factors
24: 1,2,3,4,6,8,12,24
42: 1,2,3,6,7,14,21,42
39: 1,3,13,39
136: 1,2,4,8,17,34,68,136
91: 1,7,13,91
60: 1,2,3,4,5,6,12,15,30
Prime numbers: #'s that have only 2 factors - 1 and itself
Composite numbers: #'s that have more than 2 factors
Divisibility
A is divisible by B if there's a number C that meets this requirement.
c x b = a
ex: 10 is divisible by 5 2x5=10
Divisibility Rules
Ending:
a # is divisible by 2 if it ends with..... 0,2,4,6,8
a # is divisible by 5 if it ends with..... 0,5
a # is divisible by 10 if it ends with..... 0
Sum of digits:
- add all of the digits of a # to see if it is divisible by the #
- by 3: if the sum of the digits of a # is divisible by 3, then the whole # is divisible by 3
- by 6: a # is divisible by 6, if it's divisible by 2 and 3
Last digits:
- by 4: a # is divisible by 4 if the last 2 digits form a # that's divisible by 4
- by 8: a # is divisible by 8 if the last 3 digits form a # that's divisible by 8 --> most likely will have to do long division
By 7:
- a # is divisible by 7 if you double the last digit and subtract the # from the original # (only the 100's place) to see if it's divisible by 7
By 11:
- chop method ---> chop off the last two digits and add it to the remaining #
---> if you double, you subtract
---> if you chop off, you add