Introducción
INVESTIGACIÓN DEL PROCESO DE RESOLUCIÓN DE UN SISTEMA DE ECUACIONES DE 4 INCÓGNITAS
Desglose estructurado detallado
Método de Gauss
11.- Dar solución a las ecuaciones sustituyendo valores de abajo hacia arriba
10.-Acomodamos nuestra ecuación de nueva forma y luego despejaremos sus incógnitas
9.-Realizar el ultimo uno en la ultima ecuación para que tenga solución por lo que realiza la operación, revisaremos que se forme un triangulo al final de nuestra ecuación.
8.-Dejar el siguiente uno por lo que realizaremos la operación y dejar ceros debajo de nuestro ultimo uno
7.-Dejar ceros debajo de nuestro siguiente uno por lo que se realizan las siguientes operaciones
6.-Dejar el siguiente uno por lo que realizamos la siguiente operacion
5.-Comenzamos realizar las operaciones para dejar ceros abajo del primer uno
4.-Dejar que los coeficientes de abajo del primer uno sean cero, de modo de formar un triángulo con ceros.
3.-Acomodar la ecuación que tenga uno de coeficientes como pivote en nuestra ecuacion
2.-Acomodar los coeficientes de cada variable en una matriz
1.-Pasoreconocer las variables y que esten ordenadas en columnas
Explicación de cómo funciona el método de lgauss
1.-Despejamos la misma incógnita en ambas ecuaciones
2.- Igualamos las expresiones, lo que nos permite obtener una ecuación con una incógnita
3.- Resolvemos la ecuación
4.- Sustituimos el valor obtenido en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita
5 .-Los dos valores obtenidos constituyen la solución del sistema
El método de igualación consiste en aislar una incógnita en las dos ecuaciones para igualarlas.
Este método es aconsejable cuando una misma incógnita es fácil de aislar en ambas ecuaciones.
1 Se despeja una incógnita en una de las ecuaciones
2 Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita
3 Se resuelve la ecuación
4 El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada
5 Los dos valores obtenidos constituyen la solución del sistema
El método de sustitución consiste en aislar en una ecuación una de las dos incógnitas para sustituirla en la otra ecuación.
Este método es aconsejable cuando una de las incógnitas tiene coeficiente 1.
1) Se resuelve el sistema de 4 ecuaciones con 4 incógnitas, haciendo tres combinaciones de 2 ecuaciones, para eliminar cualquiera de las incógnitas, pero que esta incógnita sea la misma en las tres combinaciones. Esto nos dará como resultado 3 ecuaciones con 3 incógnitas.
2) Formamos un Sistema de 3 ecuaciones con 3 incógnitas y procedemos a hacer dos combinaciones de 2 ecuaciones, para eliminar cualquiera de las incógnitas, pero que esta incógnita sea la misma. El resultado nos dará dos ecuaciones con 2 incógnitas.
3) Formamos un sistema de 2 ecuaciones con 2 incógnitas y procedemos a eliminar una cualquiera de las incógnitas y encontrar el valor de la otra incógnita.
4) Sustituimos el valor de la incógnita obtenido en la otra ecuación del sistema de 2 ecuaciones con 2 incógnita y encontraremos el valor de la otra incógnita.
5) Sustituimos el valor de las 2 incógnitas obtenidas en una cualquiera de las 3 ecuaciones con 3 incógnitas para encontrar el valor de una tercera incógnita.
6) Sustituimos el valor de las 3 incógnitas obtenidas en una cualquiera de las 4 ecuaciones con 4 incógnitas para encontrar el valor de la cuarta incógnita.
7) La solución general será el valor de las cuatro incógnitas obtenidos.
Explicación de cómo funciona el método de eliminación
El sistema equivalente resultante es: Sistema escalonado equivalente al anterior
Obtenemos un sistema escalonado que resolvemos por el método de sustitución hacia arriba.
De la última ecuación: –17t = 51 => t = 51/(-17) = –3
Sustituyendo el valor de t en la tercera ecuación: 12z – 13t = 87 => 12z –13(-3) = 87 => 12z = 87–39 = 48 => z = 48/12 = 4
Sustituyendo los valores de t y z en la segunda ecuación: – 4y + 4z –7t = 29 => – 4y + 4·4 – 7(–3) = 29 => – 4y + 16 + 21 = 29 => – 4y = 29 – 37 = –8 => y = –8/(–4) = 2
Por último hallamos el valor de x. Para ello en la 1ª ecuación sustituimos los valores de y, z, t ya hallados: x + 2·2 – 4 + 3·(–3) = –8 => x + 4 – 4 –9 = –8 => x = 1
Por tanto la solución del sistema es: x = 1; y = 2; z = 4; t = –3.
Vamos a beneficiarnos de las ventajas del método de Gauss para este tipo de sistemas de 4 ecuaciones con 4 incógnitas por ser el más adecuado.
Conclusiones
Ventajas y desventajas de la resolución de sistemas de ecuaciones de 4 incógnitas
Desventajas
Puede ser un proceso largo y laborioso
Requiere un alto nivel de conocimiento matemático
Ventajas
Ayuda a modelar situaciones del mundo real
Permite encontrar soluciones precisas para problemas complejos
Aplicaciones de la resolución de sistemas de ecuaciones de 4 incógnitas
En la economía
En la ingeniería
En la física
Desarrollo del proceso de resolución de un sistema de ecuaciones de 4 incógnitas
Ejemplo paso a paso de la resolución de un sistema de ecuaciones de 4 incógnitas utilizando el método de eliminación
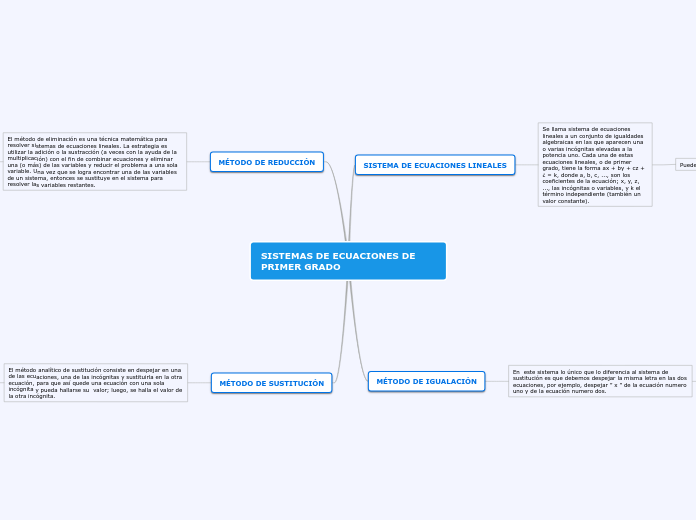
Métodos de resolución de sistemas de ecuaciones de 4 incógnitas
Método de la matriz inversa
Método de igualación
Método de sustitución
Método de eliminación
Definición de un sistema de ecuaciones de 4 incógnitas