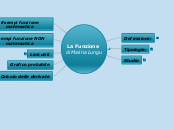
La Funzione
di Malina Lungu
Nome: Malina
Cognome: Lungu
Classe: 4°S
Scuola: "I.I.S. A. Castigliano" Asti
Anno Scolastico: 2015/2016
Calcolo delle derivate
Grafico probabile
Link utili
Testi
http://www.matematika.it/public/allegati/33/11_04_Funzioni_definizione_tipi_4_0.pdf http://www.math.it/studio_fne/classificazione.htm http://matepratica.it/2012/04/domini-di-funzioni.html http://www.youmath.it/lezioni/analisi-matematica/limiti-continuita-e-asintoti/194-asintoti-verticali.html http://www.youmath.it/lezioni/analisi-matematica/limiti-continuita-e-asintoti/193-asintoti-orizzontali.html http://www.youmath.it/lezioni/analisi-matematica/limiti-continuita-e-asintoti/197-asintoti-obliqui.html http://www.matematika.it/public/allegati/33/11_34_Asintoti_1_1.pdf
Video
https://www.youtube.com/watch?v=kDqCKm40mr8
Funzione pario o dispari
Esempi funzione NON matematica
Esempi funzione matematica
Studio
Asintoti
DEFINIZIONE: È una retta a cui tende una funzione in un comportamento limite
ORIZZONTALE
DEFINIZIONE: Si dice che un fz y=f(x) preenta un asintoto orizzontale nella retta y=l se lim x-->±∞ f(x)=l
OBLIQUO
DEFINIZIONE: È una funzione del piano cartesiano di equazione y=mx+q che aprossima il comportamento di una data funzione all'infinito
VERTICALE
DEFINIZIONE: data una funzione la retta uguale a x=Xo è asintoto della fz
Limiti
DEFINIZIONE: studiare il comportamento di una fnzione agli estremi del campo di esistenza (dominio)
CONTINUITÀ
PUNTI DI DISCONTINUITÀ
3 SPECIE
(ELIMINABILE) Esso puo': A)Non esistere B)Esistere ma risultare di valore diverso dal limite
2 SPECIE
(∞ o verticale) Se la funzione in un punto vale infinito (nfinito non e' un punto ben preciso ma una convenzione) quindi quando la funzione vale infinito non e' definita
1 SPECIE
(SALTO) Si dice di prima specie se esistono finiti i limiti destro e sinistro ma i due limiti sono diversi
DEFINIZIONE:
-IN 1 PUNTO data una fz y=f(x) definita in un introno di xo si dice continua in xo se: lim x-> xo f(x)=f(xo)
-IN 1 INTERVALLO
CALCOLO DEI LIMITI: A:i limiti della fz tenendo in considerazione ±∞ A1: lim f(x)=-4 x-->-∞
A2: lim fz(x)=+∞ x-->+∞ B:i limiti della fz in prossimità di un numero FINITO B2: lim f(x)=+∞ x-->0
Pario o dispari
Una funzione f(x) viene detta PARI quando per ogni x appartiene al dominio, cioè f(-x)=f(x) quindi ad esempio se noi calcoliamo la funzione in 4 essa deve dare lo stesso valore quando la calcoliamo in -4.
La loro caratteristica è quella di avere il grafico simmetrico rispetto all'asse delle ordinate.
La funzione f(x) è DISPARI se per ogni x appartenente al dominio vale la relazione f(-x)=-f(x) cioè se la funzione di 4 vale 7 allora quando la calcolerò in -4 dovrà valere -7, queste deve valere per ogni coppia di punti che si trovano in posizone simmetrica del dominio.
La loro caratteristica è quella di avere il grafico simmetrico rispetto all'origine.
Segno
DISEQUAZIONI
Fratte/frazionarie
Cioè di quelle disequazioni che contengono l'INCOGNITA a DENOMINATORE della frazione. Qualunque sia il tipo di disequazione frazionaria essa è sempre riconducibile al RAPPORTO tra DUE POLINOMI. Per risolvere questo tipo di disequazione è sufficiente STUDIARE il SEGNO DEL NUMERATORE e il SEGNO DEL DENOMINATORE e il SEGNO DELLA FRAZIONE.
2° Grado
Se hai un sistema di disequazioni devi semplicemente risolvere ogni disequazione e porre i risultati su un grafico: le soluzioni del sistema sono i valori validi contemporaneamente per tutte le disequazioni.
1° Grado
Il sistema si dice di primo grado quando le disequazioni che lo compongono sono di primo grado
Per risolvere un sistema basta risolvere le disequazioni che lo compongono poi considerare le soluzioni che vanno bene per tutte le disequazioni
DEFINIZIONE: Risolvere una disequazione significa trovare gli intervalli dei valori che sostituiti alla x rendono la diseguaglianza vera In una disequazione possiamo trovare solo i valori maggiori oppure minori di qualcosa
oppure possiamo trovare i valori maggiori e uguali oppure minori e uguali .
Dominio
Cioè è l’insieme su cui la funzione è definita.
Condominio
Cioè l’insieme dei valori che la funzione può assumere.
Tipologie:
funzioni trascendenti
La quale contiene operazioni trascendenti: logaritmo, esponenziale o le funzioni goniometriche.
Si articolano in LOGARITMICHE, GONIOMETRICHE ed ESPONENZIALI.
Funzione algebrica
Nella quale compaiono solo operazioni di tipo algebrico: addizione sottrazione, moltiplicazione, divisione, potenza.
Essa può dividersi in:
RAZIONALE e IRRAZIONALI
che si dividono a loro volta in fratte e intere.
Definizione:
E' una relazione tra i due insiemi, A e B. La funzione dell'Insieme A e dell'insieme B è una funzione che ad ogni elemento di A associa uno e uno solo elemento di B.
OPPURE
Dati due insiemi X e Y, si dice funzione da X in Y una relazione che associa ad ogni elemento dell'insieme X, detto dominio, un unico elemento dell'insieme Y detto condominio.